Vierecke - Eigenschaften und Arten
Das Viereck ist eine der bekanntesten Figuren der Mathematik. Es kann in vielen verschiedenen Formen auftreten, doch alle haben ein paar Eigenschaften gemeinsam. In diesem Text wollen wir uns mit den unterschiedlichen Formen von Vierecken befassen und die gemeinsamen Eigenschaften herausarbeiten.
Viereck allgemein
Das Viereck hat, wie der Name schon verrät, vier Ecken. Diese vier Ecken bzw. 4 Punkte, werden in alphabetischer Reihenfolge mit Großbuchstaben benannt, also mit A, B, C und D.
Ein Beispiel für ein Viereck zeigt die folgende Abbildung:
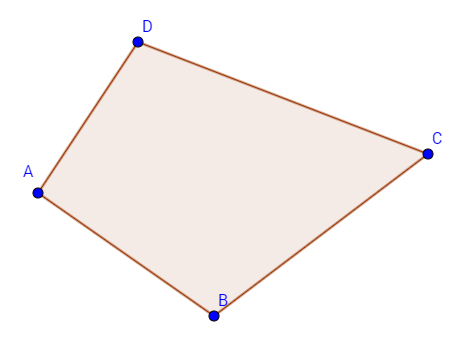
Ein allgemeines Viereck wird ein Viereck genannt, was keine besondere Form hat, sondern einfach nur vier Ecken. Die Eigenschaften jedes Viereckes sind also:
Merke
Eigenschaften von allen Vierecken:
Vierecke haben vier Linien, die vier Ecken miteinander verbinden.
Die vier Ecken werden Punkte genannt und alphabetisch benannt.
Die Seiten werden auch alphabetisch benannt. Die Namen werden hierbei klein geschrieben, um eine Verwechslung mit den Punkten zu vermeiden.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Sonderformen von Vierecken
Das Viereck ist eine der vielseitigsten geometrischen Figuren. Daher gibt es auch mehrere Sonderformen, die wir hier kurz erwähnen wollen.
Das Parallelogramm
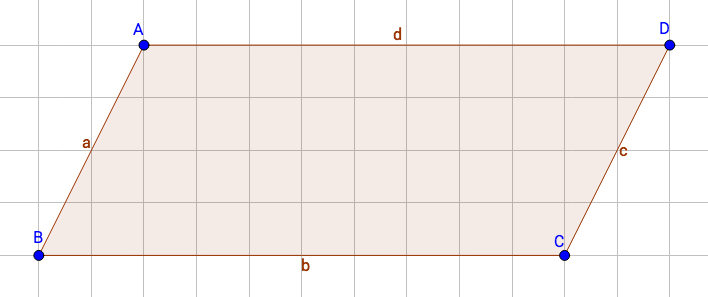
Das Parallelogramm hat die gleichen Eigenschaften wie das allgemeine Viereck. Im Namen Parallelogramm steckt aber auch die besondere Eigenschaft dieses Vierecks: Die gegenüberliegenden Seiten sind immer parallel.
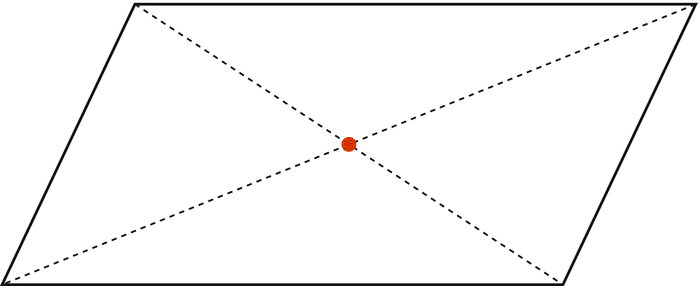
In dieser Abbildung siehst du ein Parallelogramm. Die linke und die rechte Seite sind parallel zueinander, genauso die obere und die untere Seite. Diese gegenüberliegenden Seiten sind zudem gleich lang. Von den Eckpunkten aus sind zwei Diagonalen gestrichelt eingezeichnet.
Das Rechteck
Das Rechteck sieht dem Parallelogramm sehr ähnlich. Die gegenüberliegenden Seiten sind auch parallel, jedoch hat das Rechteck in allen Eckpunkten immer rechte Winkel, wie wir in der folgenden Abbildung erkennen können:
Das Quadrat
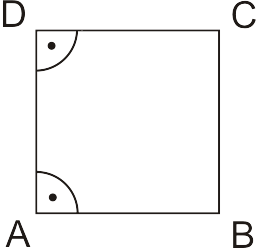
Das Quadrat ist eine besondere Form des Rechtecks. Beim Quadrat sind die gegenüberliegenden Seiten auch parallel und in allen Eckpunkten befinden sich auch rechte Winkel. Die Besonderheit im Vergleich zum Rechteck ist die Seitenlänge. Bei einem Rechteck sind die jeweils gegenüberliegenden Seiten gleich lang und bei einem Quadrat haben alle vier Seiten die gleiche Länge. Ein Quadrat zeigt sich in der folgenden Abbildung:
Merke
Eigenschaften der Sonderformen:
Beim Parallelogramm sind die gegenüberliegenden Seiten parallel.
Beim Rechteck sind nicht nur die gegenüberliegenden Seiten parallel, sondern jeder Winkel im Rechteck ist ein rechter Winkel.
Beim Quadrat sind nicht nur die gegenüberliegenden Seiten parallel und die Winkel alle rechtwinklig, sondern die Seitenlängen aller Seiten gleich groß.
Zur Vertiefung dieses Themas schau dir auch noch einmal die Übungen an!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
