So konstruierst du Umkreis und Inkreis eines Dreiecks
Neben Seiten und Winkeln können wir an Dreiecken auch den sogenannten Inkreis und den Umkreis bestimmen. Diese Kreise können wir allerdings nicht einfach aus der Figur ablesen, sondern müssen sie zunächst selbstständig konstruieren.
Inkreis eines Dreiecks
Merke
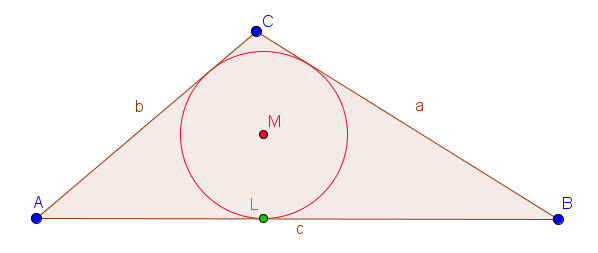
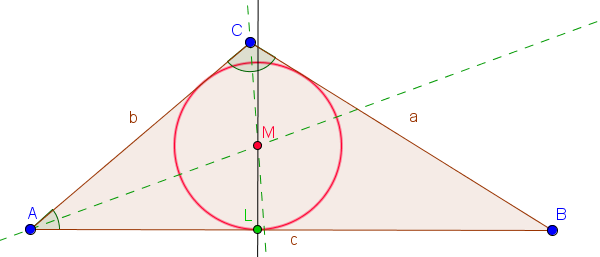
Der Inkreis eines Dreiecks ist ein Kreis, der alle Seiten des Dreiecks von innen einmal berührt. Die Seiten des Dreiecks sind in diesem Fall also Tangenten des Kreises. Der Mittelpunkt des Kreises ergibt sich aus dem Schnittpunkt der Winkelhalbierenden.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Konstruktion eines Inkreises
Um einen Inkreis zu konstruieren, gehen wir folgendermaßen vor:
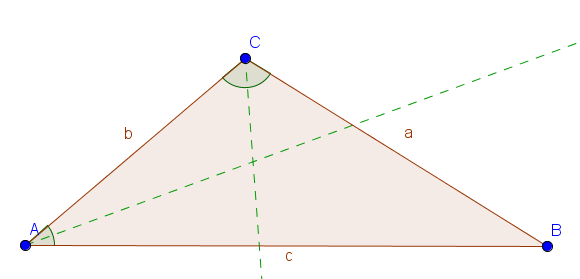
1. Schritt: Winkelhalbierende einzeichnen
Die Winkelhalbierende ist eine Halbgerade (oder auch Strahl), die im Scheitelpunkt eines Winkels entspringt und den Winkel in zwei gleich große Teile teilt. Da Dreiecke drei Winkel besitzen, können wir also insgesamt drei Winkelhalbierende einzeichnen. Zur Konstruktion der Winkelhalbierenden benötigst du einen Zirkel. Wenn du nicht mehr genau weißt, wie man Winkelhalbierende einzeichnet, kannst du es in unserem Erklärtext zur Konstruktion einer Winkelhalbierenden nachlesen.
Um den Schnittpunkt der drei Winkelhalbierenden zu bestimmen, genügt es zwei der drei Halbgeraden einzuzeichnen.
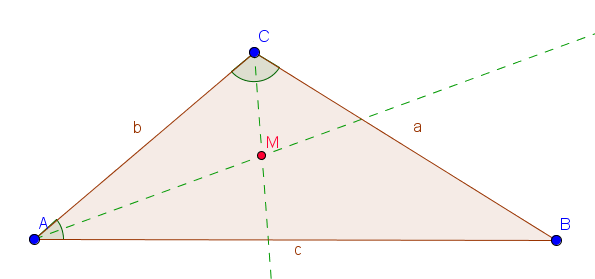
2. Schritt: Schnittpunkt markieren
Den Schnittpunkt der Winkelhalbierenden können wir nun einfach ablesen und haben somit den Mittelpunkt ($M$) des Kreises.
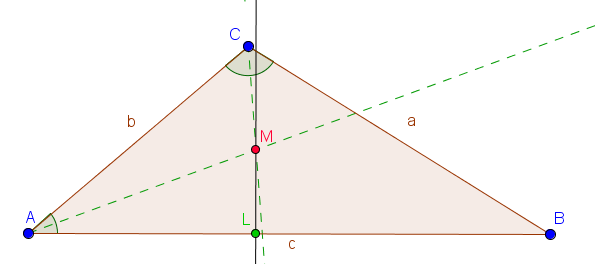
3. Schritt: Ein Lot von einer Seite des Dreiecks durch den Schnittpunkt zeichnen
Den Mittelpunkt des Inkreises haben wir nun schon eingezeichnet. Um den Kreis konstruieren zu können, fehlt uns nur noch der Radius. Dazu fällen wir ein Lot von einer Seite des Dreiecks (in diesem Fall $c$) durch den Mittelpunkt. Der Abstand zwischen Lotfußpunkt ($L$) und Mittelpunkt ($M$) ist der Radius des Inkreises.
In unserem Erklärtext zum Thema Lot fällen kannst du noch einmal nachlesen, wie du ein Lot einzeichnest.
4. Schritt: Inkreis einzeichnen
Wir haben nun sowohl den Mittelpunkt als auch den Radius gegeben und können den Kreis einzeichnen.
Umkreis eines Dreiecks
Merke
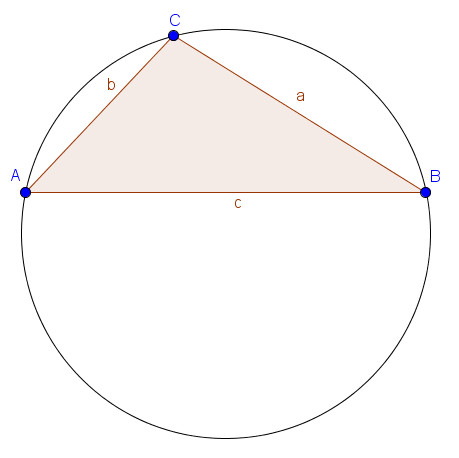
Der Umkreis eines Dreiecks geht durch alle drei Eckpunkte des Dreiecks. Sein Mittelpunkt ist der Schnittpunkt der Mittelsenkrechten.
Konstruktion eines Umkreises
Um den Umkreis eines Dreiecks zu konstruieren, gehen wir wie folgt vor:
1. Schritt: Mittelsenkrechten einzeichnen
Ein Dreieck besitzt drei Mittelsenkrechten, die jeweils senkrecht auf den Seiten des Dreiecks stehen. Um die Mittelsenkrechten zu konstruieren, benötigst du einen Zirkel. Wenn du nicht mehr weißt, wie man eine Mittelsenkrechte einzeichnet, solltest du in unserem Lerntext zum Thema Mittelsenkrechten konstruieren noch einmal üben.
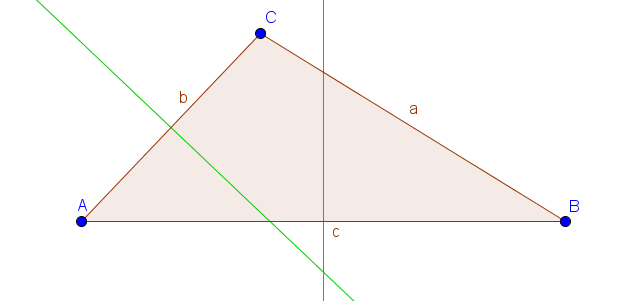
Es genügt, zwei der drei Mittelsenkrechten einzuzeichnen, um den Schnittpunkt ablesen zu können.
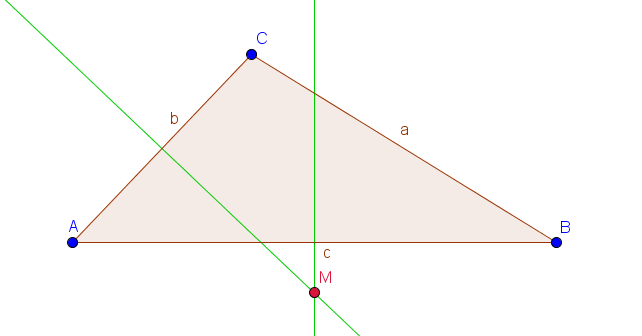
2. Schritt: Schnittpunkt einzeichnen
Den Schnittpunkt der Mittelsenkrechten können wir einfach ablesen. Er entspricht dem Mittelpunkt des Umkreises und kann inner- oder außerhalb des Dreiecks liegen.
3. Schritt: Kreis einzeichnen
Wie schon beim Inkreis, fehlt uns nun noch der Radius des Kreises. Glücklicherweise können wir diesen auch einfach ablesen. Der Radius des Umkreises ist der Abstand des Mittelpunkts zu den drei Eckpunkten. Wir zeichnen den Kreis also einfach durch einen der Eckpunkte des Dreiecks.
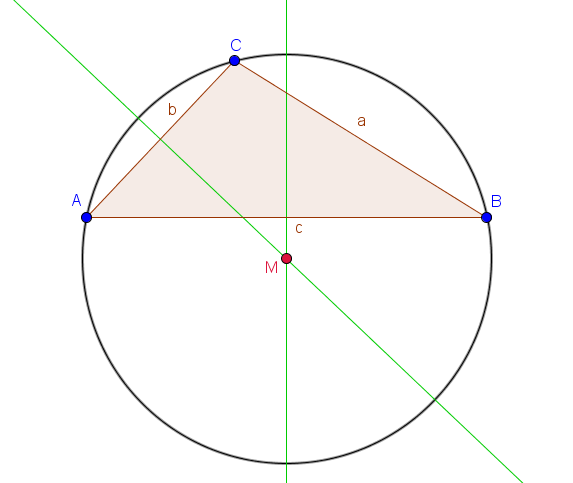
Besondere Fälle
Je nach Art des Dreiecks lassen sich verschiedene Spezialfälle unterscheiden:
- Bei spitzwinkligen Dreiecken liegt der Mittelpunkt des Umkreises immer innerhalb des Dreiecks.
- Bei rechtwinkligen Dreiecken ist der Mittelpunkt des Umkreises gleichzeitig der Mittelpunkt der Hypotenuse.
- Bei stumpfwinkligen Dreiecken liegt der Mittelpunkt des Umkreises immer außerhalb des Dreiecks.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Viel Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
