Besondere & ausgezeichnete Punkte im Dreieck
In einem Dreieck gibt es bestimmte Punkte, die man für verschiedene Berechnungen benötigt. Diese sogenannten ausgezeichneten Punkte des Dreiecks können nicht einfach aus dem Dreieck abgelesen werden, sondern werden mithilfe geometrischer Konstruktionen am Dreieck bestimmt. Schauen wir uns nun die vier klassischen ausgezeichneten Punkte eines Dreiecks näher an.
Höhenschnittpunkt ($H$)
Die Höhe eines Dreiecks ist ein Lot, dass von einem Eckpunkt des Dreiecks auf die gegenüberliegende Seite gefällt wird. Dementsprechend besitzt ein Dreieck drei unterschiedliche Höhen. Der Schnittpunkt dieser drei Höhen ist der sogenannte Höhenschnittpunkt, den man mit $H$ bezeichnet.
Merke
Der Höhenschnittpunkt $H$ ist der Schnittpunkt aller drei Höhen eines Dreiecks.
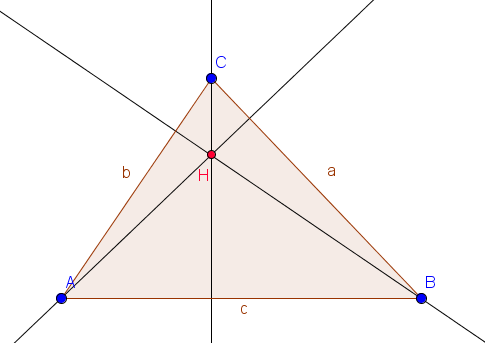
In einem spitzwinkligen Dreieck liegt der Höhenschnittpunkt innerhalb des Dreiecks. Hat das Dreieck einen stumpfen Winkel (über $90°$) liegt $H$ außerhalb des Dreiecks. In einem rechtwinkligen Dreieck stimmt der Höhenschnittpunkt mit dem Scheitel des rechten Winkels überein.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Umkreismittelpunkt ($U$)
Der Umkreismittelpunkt eines Dreiecks wird mithilfe der Mittelsenkrechten konstruiert. Das Dreieck besitzt pro Seite eine Mittelsenkrechte. Der Schnittpunkt der drei Mittelsenkrechten ist der Mittelpunkt des Umkreises. Dieser Umkreis hat zu allen Eckpunkten des Dreiecks denselben Abstand.
Merke
Der Umkreismittelpunkt $U$ ist der Schnittpunkt aller drei Mittelsenkrechten eines Dreiecks.
Inkreismittelpunkt ($I$)
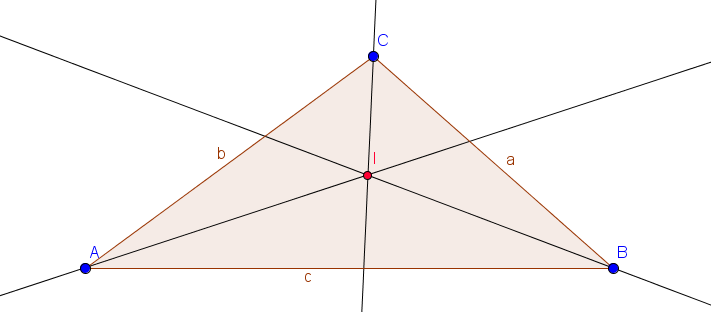
Der Inkreis eines Dreiecks ist ein Kreis, der alle Seiten des Dreiecks von innen berührt. Der Mittelpunkt dieses Kreises ist der Schnittpunkt aller Winkelhalbierenden. Eine Winkelhalbierende ist eine Halbgerade, die einen Winkel in zwei gleich große Teile teilt. Lerne hier mehr über das Einzeichnen von Winkelhalbierenden.
Merke
Der Inkreismittelpunkt $I$ ist der Schnittpunkt der Winkelhalbierenden eines Dreiecks.
Schwerpunkt ($S$)
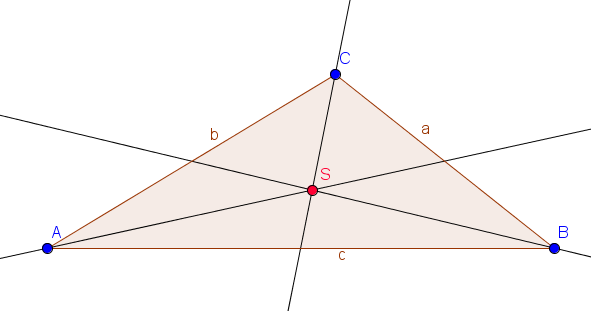
Der Schwerpunkt ist eine Art Mittelwert. Er ist der Punkt, an dem die die Fläche des Dreiecks im Gleichgewicht steht. Wir könnten ein ausgeschnittenes Dreieck also mit seinem Schwerpunkt auf eine Bleistiftspitze setzen und es würde nicht herunterfallen. Um den Schwerpunkt des Dreiecks zu bestimmen, müssen wir die Seitenhalbierenden des Dreiecks konstruieren. Die Seitenhalbierenden des Dreiecks sind Strecken, die einen Eckpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbinden. Der Schnittpunkt aller drei Seitenhalbierenden ist der Schwerpunkt des Dreiecks.
Merke
Der Schwerpunkt $S$ ist der Schnittpunkt der Seitenhalbierenden eines Dreiecks.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben. Viel Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
