Was ist eine Strecke, eine Halbgerade und eine Gerade?
Dieser Text beschäftigt sich mit den Begriffen Punkt, Gerade, Halbgerade und Strecke. Hier wird also einzeln aufgeschlüsselt wofür du und wie du alles bestimmst und benutzen kannst.
Was ist ein Punkt?
Mehrere Punkte bilden in der Mathematik eine geometrische Figur. Definiert wird der Punkt als Schnittstelle zweier Geraden.
Merke
Merke
Der Punkt ist die Schnittstelle zweier Geraden. Er ist starr und hat keine Ausdehnung, wie etwa eine Linie.
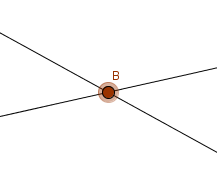
Was ist eine Strecke?
Die Strecke ist in der Geometrie eine Linie, die zwei Punkte verbindet. Diese Linie ist die kürzeste Verbindung zwischen den beiden Punkten. Die Punkte, die eine Strecke definieren, nennt man auch Start- bzw. Endpunkte.
Merke
Merke
Eine Strecke ist eine Linie, die zwei Punkte auf kürzestem Wege verbindet.
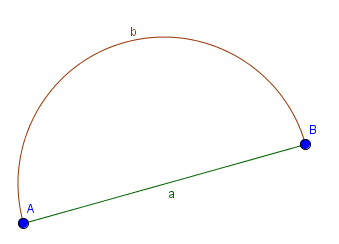
Bei der Abbildung oben erkennen wir die Linien a und b. Diese verbinden die Punkte A und B miteinander. Jedoch ist nur die Linie a auch eine Strecke, da sie den kürzesten Abstand zwischen den beiden Punkten bildet. Die Verbindungslinie b ist ein Halbkreis, l dieser hat nicht den kürzesten Abstand zwischen A und B.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Halbgerade und Gerade
Merke
Merke
Eine Halbgerade auch Strahl genannt hat einen Startpunkt, aber keinen Endpunkt hat.
Eine Halbgerade ist eine Gerade, die an einem bestimmten Punkt beginnt, aber kein Ende hat. Sie geht ins Unendliche. Später wird diese Form der geometrischen Darstellung auch unter dem Begriff Strahl vorkommen, etwa bei den Strahlensätzen.
In der folgenden Abbildung wird ein Strahl, bzw. eine Halbgerade dargestellt.
Merke
Merke
Eine Gerade ist eine geometrische Figur die unendlich lang, unendlich dünn und in beide Richtungen unbegrenzt ist.
Eine Gerade ist also eine Strecke, die über die beiden Punkte hinaus geht, somit weder Start- noch Endpunkt haben. Wenn wir eine Gerade zeichnen wollen, zeichnen wir eine Strecke zwischen zwei Punkten und gehen dann mit der Linie über die beiden Punkte hinaus, um eine Gerade zu erhalten.
Die Lage von Geraden zueinander
Wenn wir zwei Geraden in einem Koordinatensystem eintragen, können diese genau drei verschiedene Beziehungen zueinander haben.
Eine Möglichkeit ist, dass Geraden zueinander parallel sind. Hierbei treffen sich die beiden Geraden niemals, egal wo sie im Koordinatensystem betrachtet werden.
Sie können aber auch gleich sein. Hierbei entsprechen sich die beiden Geraden und haben somit unendlich viele Schnittpunkte.
Die letzte Möglichkeit sind sich schneidende Geraden. Hierbei treffen die Geraden aufeinander und bilden einen Schnittpunkt. Ein Spezialfall sind orthogonale Geraden. Hierbei treffen zwei Geraden in einem 90° Winkel aufeinander.
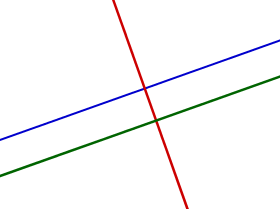
In der Abbildung sind die grüne und die blaue Gerade parallel zueinander. Die rote Gerade ist orthogonal zu den beiden anderen Geraden, hat also jeweils einen Schnittpunkt mit beiden.
Dein neu erlerntes Wissen kannst du mit unseren Übungsaufgaben festigen. Viel Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
