Flächeninhalt und Umfang von Dreiecken berechnen
Das Dreieck gilt als die einfachste zweidimensionale, geometrische Figur, da es lediglich durch drei Punkte definiert wird. Aber lasst euch nicht täuschen: auch wenn das Dreieck als die vermeintlich einfachste Figur gilt, sind die Berechnungen nicht immer einfach. Dazu kommt noch, dass man zwischen mehreren Arten von Dreiecken unterscheidet. Schauen wir uns zunächst eine allgemeine Darstellung an.
Größen im Dreieck: Punkte, Seiten und Winkel
Die großen Buchstaben stehen für die einzelnen Eckpunkte. Für unsere Berechnungen sind diese Punkte noch nicht ganz so wichtig, bei fortgeschrittenen Problemen werden sie für euch aber unverzichtbar, weshalb es Sinn macht sie direkt mitzulernen. Die kleinen Buchstaben entsprechen den einzelnen Seiten. Wichtig ist dabei, dass die Seiten nach den gegenüberliegenden Punkten benannt werden. Schaust du dir beispielsweise den Punkt $B$ an, wirst du feststellen, dass keine der Seiten, die von Punkt $B$ ausgehen, mit $b$ benannt sind, sondern diejenige Seite, die dem Punkt gegenüber liegt.
In einem Dreieck ist aber noch eine andere Größe entscheidend: der Winkel. Dieser richtet sich wiederum nach dem Punkt, aus dem er hervorgeht (ganz im Gegensatz zu den Seitenlängen, wie du eben gelernt hast). Die Winkel werden mit den entsprechenden griechischen Buchstaben benannt (alpha, beta, gamma etc.).
Merke
In einem Dreieck ist die Summe der Innenwinkel immer 180° - nie weniger und nie mehr!
Das Rechnen mit Winkeln im Dreieck wird Bestandteil eines anderen Kapitels sein, weshalb wir uns im Moment noch nicht detailliert mit ihnen beschäftigen werden. Spätestens beim Satz des Pythagoras sind diese aber unumgänglich.
Verschiedene Dreiecks-Typen
Je nachdem in welchem Verhältnis die Seitenlängen zueinander stehen, unterscheiden wir verschiedene Dreiecks-Typen:
Beispiel
1. Ungleichseitiges Dreieck
Die allgemeine Darstellung eines Dreiecks, die du bereits kennengelernt hast, entspricht einem ungleichseitigen Dreieck. Es gilt $a \neq b \neq c$
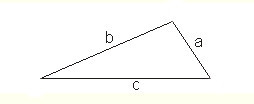
Beispiel
2. Gleichseitiges Dreieck
Bei einem gleichseitigen Dreieck sind alle Seiten gleich. Es gilt $a = b = c$
Beispiel
3. Gleichschenkliges Dreieck
Bei einem gleichschenkligen Dreieck sind nur zwei Seiten gleich. Die von der Spitze des Dreiecks ausgehenden Seiten bezeichnet man als Schenkel. Bei einem gleichschenkligen Dreieck sind genau diese Seiten gleich lang. Es gilt $a = b \neq c$
Umfang eines Dreiecks
Die Berechnung von Flächeninhalt und Umfang ist bei allen Dreiecken gleich. Und auch hier ist der Umfang deutlich einfacher zu berechnen. Du musst nur die einzelnen Seitenlängen addieren.
Merke
Der Umfang $U$ eines Dreiecks berechnet sich durch die Addition der Seitenlängen.
$U = a + b + c$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Flächeninhalt eines Dreiecks
Für den Flächeninhalt formen wir das Dreieck, wie schon beim Parallelogramm so um, dass sich eine bereits bekannte Figur ergibt. Da man ein Dreieck selbst wieder nur in Dreiecke zerlegen kann, wenden wir dieses Mal eine etwas andere Methode an. Wir nehmen einfach zwei Dreiecke und legen sie so aneinander, dass eine viereckige Figur entsteht. Probiere das doch einmal selbst aus.
Wie du siehst, erhalten wir ein Parallelogramm. Dazu wird ein Dreieck um 180° gedreht. Anschließend werden beide Dreiecke zusammengesetzt. Wie du den Flächeninhalt des entstandenen Parallelogramms ausrechnest, weißt du ja bereits.
Gehen wir von einem Dreieck aus, dass an der Seite $b$ zusammengeführt wurde (s. Abbildung) erhalten wir für den Flächeninhalt des Parallelogramms $A= c\cdot h_{c}$.
Methode
Vorsicht mit dem Begriff der Höhe.
Beachte bitte, dass wir hier von der Höhe auf die Seitenlänge c sprechen. Wie du weißt, gibt es genauso viele Höhen in einem Parallelogramm oder Dreieck, wie es unterschiedliche Seiten gibt. Sollte dir das neu vorkommen, musst du unbedingt das Kapitel wiederholen, indem wir uns mit Parallelogrammen beschäftigt haben.
Da das Parallelogramm aus insgesamt zwei Dreiecken besteht, musst du den erhaltenen Wert noch durch 2 teilen. Genauso gut funktioniert es, wenn du die Gleichung mit 0,5 multiplizierst.
Merke
Den Flächeninhalt $A$ eines Dreiecks errechnet sich aus der halben Grundseite mal der Höhe. Da nicht immer klar ist, was genau die Grundseite ist, können wir diese Regel auch allgemeiner formulieren:
$A = \frac{1}{2} \cdot (a \cdot h_{a})$
$A = \frac{1}{2} \cdot (b \cdot h_{b})$
$A = \frac{1}{2} \cdot (c \cdot h_{c})$
Sonderfall: Flächeninhalt eines rechtwinkligen Dreiecks
Bei einem rechtwinkligen Dreieck, das heißt einem Dreieck bei dem einer der drei Winkel 90° beträgt, kann man den Flächeninhalt noch einfacher berechnen. Aus einem solchen Dreieck ergibt sich nämlich eine ganz besondere Form des Parallelogramms, die du bereits kennst: ein Rechteck.
Auch hier gilt natürlich: Der Flächeninhalt des Dreiecks ist der halbe des Rechtecks.
Merke
Der Flächeninhalt $A$ eines rechtwinkligen Dreiecks berechnet sich aus der Hälfte des Produktes der am rechten Winkel anliegenden Seiten.
$A = \frac{1}{2} \cdot (a \cdot b)$
Der Umfang $U$ errechnet sich genauso wie bei anderen Dreiecken.
Vertiefe das Wissen jetzt in den Übungsaufgaben. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
