Trapez: Flächeninhalt und Umfang berechnen
Schauen wir uns einen besonderen Fall eines Parallelogramms an: das Trapez. Im Prinzip handelt es sich dabei um ein Parallelogramm, dessen Grundseiten nicht mehr gleich lang sind. Daraus ergibt sich eine sehr verzerrte Figur:
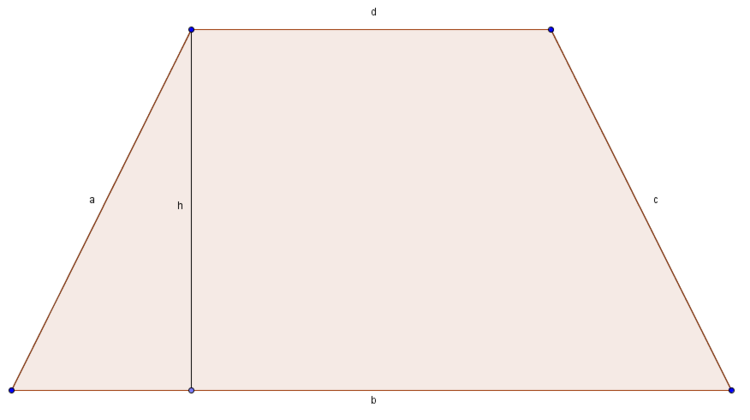
Umfang eines Trapezes
Wie schon bei vielen Figuren zuvor, kannst du den Umfang denkbar einfach berechnen, indem du einfach die Seitenlängen addierst.
Merke
Der Umfang $U$ eines Trapezes berechnet sich durch die Addition der Seitenlängen:
$U = a + b +c +d$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Flächeninhalt eines Trapezes
Auch wenn das Trapez eine große Ähnlichkeit zum Parallelogramm hat, stoßen wir bei der Berechnung des Flächeninhalts auf ein Problem. Erinnerst du dich noch daran, wie wir den Flächeninhalt eines Parallelogramms errechnen konnten? Wir konnten an einer Seite ein Dreieck abschneiden und so an der anderen Seite platzieren, dass ein Rechteck entsteht.
Da beim Trapez die gegenüberliegenden Seiten nicht gleich lang sind, können wir diese Methode jetzt nicht mehr anwenden. Wie schon beim Dreieck bleibt uns nichts anderes übrig, als mehrere Trapeze zu einer bekannten Figur zusammenführen. Dabei setzen wir zwei Trapeze an derselben Kante zusammen. Probiere es einmal aus!
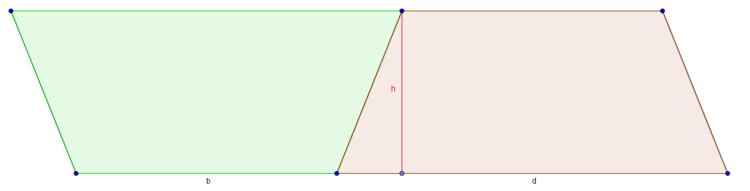
Durch die Drehung erhalten wir ein Parallelogramm, dessen Höhe der Höhe des Trapezes entspricht. Jetzt müssen wir nur noch den Flächeninhalt des Parallelogramms berechnen, was wir ja schon geübt haben und die erhaltene Fläche durch zwei teilen, da wir das Trapez ja auch zweimal in das Parallelogramm verbaut haben.
Methode
Erinnerst du dich an die Berechnung eines Flächeninhaltes im Parallelogramm?
Für den Flächeninhalt $A$ eines Parallelogramms gilt:
$A= a\cdot h_{a}$, wobei $a$ der Grundseite entspricht.
Die Höhe ändert sich durch die Transformation nicht und kann einfach aus dem ursprünglichen Trapez genommen werden. Bei der entsprechenden Seitenlänge musst du aber aufpassen:
Wie du siehst, setzt sich die Seite, auf die die Höhe fällt, aus den Seiten $b$ und $d$ zusammen.
Merke
Der Flächeninhalt eines Trapezes berechnet sich wie folgt:
$A = \frac{1}{2} \cdot (b + d) \cdot h$
Dabei entspricht $b$ der Grundseite und $d$ der Oberkante. Beachte, dass Oberkante und Grundseite in anderen Aufgaben unterschiedlich benannt sein können!
In den Übungsaufgaben kannst du jetzt dein neues Wissen überprüfen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
