Regelmäßige Vielecke konstruieren und berechnen
In diesem Text erklären wir dir, welche Arten von Vielecken es gibt und wie du den Flächeninhalt und Umfang berechnen kannst.
Regelmäßige Vielecke
Die bekanntesten Vielecke sind regelmäßige Vielecke. Die Besonderheit an ihnen ist, dass alle Seiten gleich lang sind und alle Innenwinkel gleich groß.
Schauen wir uns zwei Beispiele an: ein Fünfeck und ein Achteck.
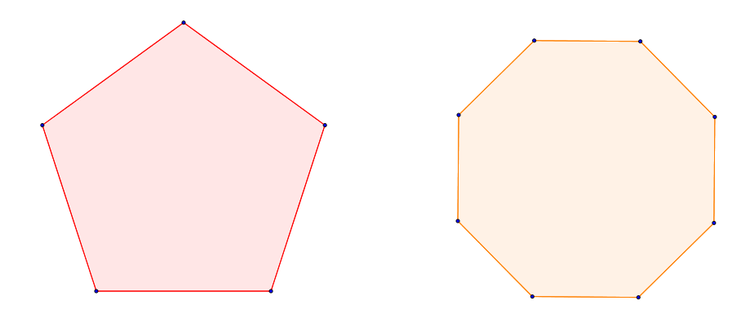
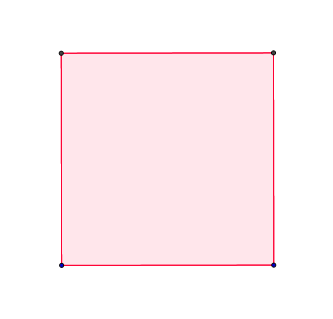
Vielleicht siehst du es nicht auf den ersten Blick, aber bei einem regelmäßigen Viereck haben alle Seiten die gleiche Länge und auch der Winkel zwischen den Seiten ist jeweils der gleiche.
Formeln zur Berechnung von Flächeninhalt, Umfang und Innenwinkel
Hier bekommst du eine Übersicht über alle wichtigen Formeln:
Methode
Flächeninhalt:
$A = \frac{n \cdot a^2}{4 \cdot tan ( \frac{180^\circ}{n})}$
Umfang:
$U = n \cdot a$
Innenwinkel:
$\alpha = \frac {n-2}{n} \cdot 180^\circ$
Dabei ist $n$: Anzahl der Ecken oder der Seiten und $a$: Seitenlänge.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispielaufgabe
Berechne mit der Angabe den Flächeninhalt und die Innenwinkel.
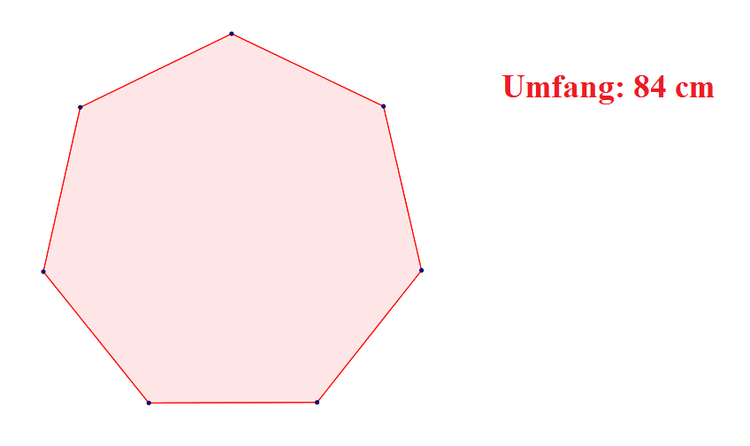
Versuche den Flächeninhalt und die Größe der Innenwinkel zu berechnen. Gegeben ist der Umfang. Er beträgt $U = 84 cm$. Wenn du nicht weiter weißt, kannst du dir die Lösung anschauen.
Vertiefung
Lösung
Der Umfang ist gegeben, er beträgt $84 cm$. Außerdem können wir die Seiten in der Abbildung zählen. Damit können wir dann die Seitenlänge berechnen.
$U = n \cdot a$ $| :n$
$a = \frac {U}{n}$
Also zählen wir zuerst die Seiten oder die Ecken. Es sind insgesamt $7$ Stück. Anschließend können wir die Länge einer Seite ($a$) berechnen:
$a = \frac {U}{n} = \frac {84 cm}{7} = 12 cm$
Wir kennen: $n = 7$ und $a = 12 cm$. Diese müssen wir nun einfach in die anderen beiden Formeln einsetzen.
Flächeninhalt:
$A = \frac{n \cdot a^2}{4 \cdot tan ( \frac{180^\circ}{n})} = \frac{7 \cdot (12 cm)^2}{4 \cdot tan ( \frac{180^\circ}{7 }) } = \frac {1008 cm^2}{1,93} = 522,25 cm^2$
Innenwinkel:
$\alpha = \frac {n-2}{n} \cdot 180^\circ = \frac {7-2}{7} \cdot 180^\circ \approx 128,57 ^\circ $
Erklärung der Formeln
Schauen wir uns hier die Herleitungen für die Formeln vom Umfang und von den Innenwinkeln an:
Umfang
Die Herleitung für den Umfang ist ganz einfach. Denn es müssen einfach die Längen der Seiten zusammengerechnet werden. Demnach ist der Umfang gleich der Anzahl der Seiten mal der Seitenlänge $\rightarrow U = n \cdot a$.
Innenwinkel
Wie kann der Innenwinkel berechnet werden? Starten wir mit dem einfachsten Vieleck, einem Dreieck.
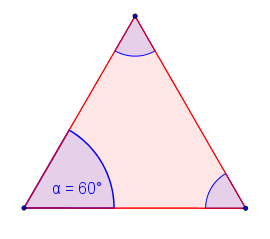
Wir wissen, dass die Innenwinkelsumme, das heißt die Summe aller Winkel zwischen den Seiten, $180 ^\circ$ groß ist. Da ein gleichseitiges Dreieck drei gleich große Winkel hat, muss diese Zahl nun durch drei geteilt werden. $\rightarrow \frac{180^\circ}{3}= 60 ^\circ $
Der Winkel zwischen den Seiten beträgt jeweils $60°$.
Die Größe der Innenwinkelsumme eines beliebigen Vielecks (also auch in nicht regelmäßigen Vielecken) berechnet man mit der Formel:
Innenwinkelsumme $= (n-2) \cdot 180^\circ $
Dabei ist $n$ die Anzahl der Ecken.
Beispiel
Innenwinkelsumme
Viereck:
Innenwinkelsumme $= (n-2) \cdot 180^\circ$ = $(4-2) \cdot 180^\circ$ = $2 \cdot 180 ^\circ$ = $360 ^\circ$
Siebeneck:
Innenwinkelsumme $= (n-2) \cdot 180^\circ$= $(7-2) \cdot 180^\circ$ = $5 \cdot 180 ^\circ$ = $900^\circ$
Die Innenwinkelsumme muss nun immer durch die Anzahl der Ecken geteilt:
Innenwinkel = Innenwinkelsumme / Anzahl der Ecken
Innenwinkel $= \frac {(n-2) \cdot 180 ^\circ}{n}$
Damit haben wir die Formeln für die Innenwinkelsumme hergeleitet.
Mit den Übungsaufgaben kannst du dich prüfen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
