In diesem Text erklären wir dir, wie du den Flächeninhalt und den Umfang von zusammengesetzten Flächen berechnen kannst.
Zusammengesetzte Flächen sind, wie der Name schon sagt, Flächen, die aus mehreren einzelnen Flächen zusammengesetzt wurden. Die nachfolgende Abbildung zeigt eine Fläche, die aus einem Dreieck, einem Quadrat, einem Rechteck, einem Parallelogramm und einem Kreis zusammengesetzt ist.
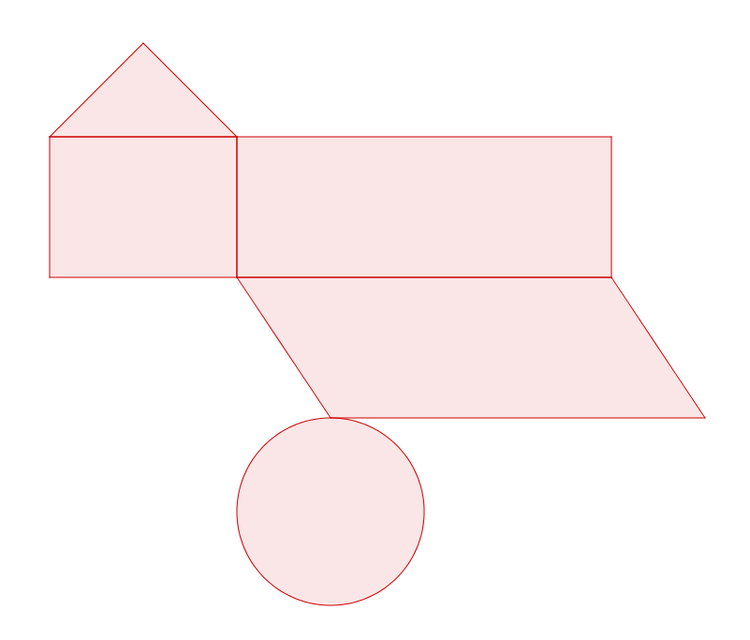
Bei der Abbildung sind die verschiedenen Flächen schon unterteilt. Die größte Schwierigkeit ist es nämlich, die Fläche, die aus verschiedenen Flächen zusammengesetzt wurde, zu unterteilen. Die einzelnen Teile der Flächen nennt man dann Teilflächen.
Flächeninhalt
Den Flächeninhalt einer zusammengesetzten Fläche zu berechnen, ist ganz einfach. Wir gehen wie folgt vor:
- Die Teilflächen identifizieren.
- Den Flächeninhalt der jeweiligen Teilflächen berechnen.
- Die Flächeninhalte addieren.
Um die Flächeninhalte richtig zu berechnen, solltest du die Formeln für verschiedene Flächen kennen.
Formeln Flächeninhalt
Merke
| Körper | Flächeninhalt | |
| Quadrat | Seitenlänge $a$ | $A = a^2$ |
| Rechteck | Seitenlängen $a, b$ | $A = a\cdot b$ |
| Dreieck | Grundseite $g$, Höhe $h$ | $A = \frac {1}{2} g \cdot h$ |
| Kreis | Radius $r$ | $A = r^2 \cdot \pi$ |
| Parallelogramm | Seitenlänge $a$ Höhe $h$ | $A =a \cdot h $ |
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Beispielaufgabe Flächeninhalt
Familie Wunsch baut ein Haus. Der tatenreiche Vater möchte selbst den neuen Boden verlegen und fragt sich, wie groß die gesamte Fläche ist. Kannst du ihm helfen?
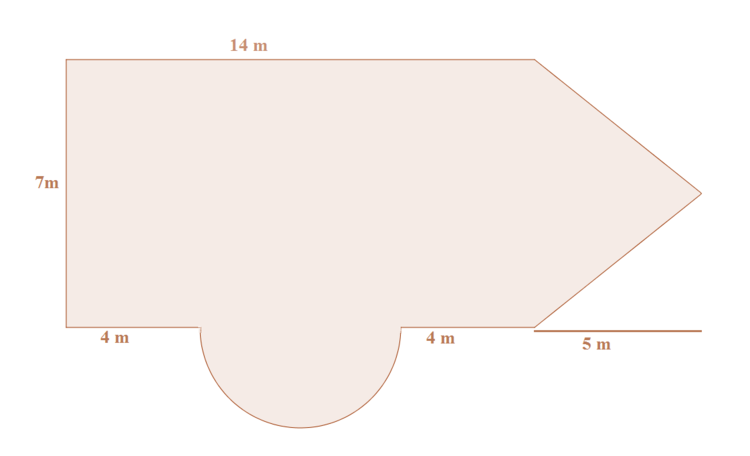
Als erstes teilen wir die Fläche in verschiedene Teilflächen ein. Schaue dir dafür die Fläche an und teile sie ein:
Vertiefung
Lösung
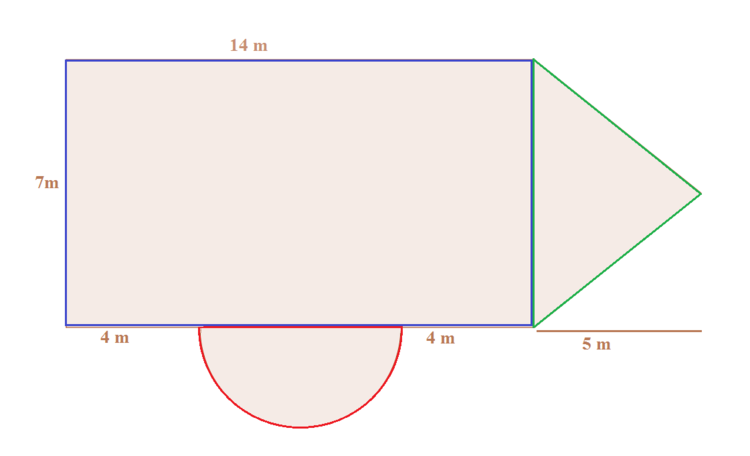
Nun müssen wir die Größe der Teilflächen berechnen.
Rechteck:
Länge mal Breite: $7 m \cdot 14 m = 98 m^2$
Halbkreis:
$\frac{1}{2}$ Radius $^2$ mal Pi: $\frac{1}{2}r^2 \pi = \frac{1}{2} \cdot (3 m)^2 \cdot \pi \approx 14,14 m^2$
Dreieck:
$\frac{1}{2}$ Grundseite mal Höhe: $\frac{1}{2} \cdot 7m \cdot 5m = 17,5 m^2$
Um die gesamte Fläche zu bestimmen, müssen die Teilflächen zusammengerechnet werden:
$98 m^2 + 14,14 m^2 + 17,5 m^2 = 129,64 m^2 $
Die gesamte Fläche beträgt $ 129,64 m^2$.
Umfang
Um den Umfang einer zusammengesetzten Fläche zu bestimmen, müssen wir jeweils die Längen der außenliegenden Teilflächen zusammenrechnen.
Beispielaufgabe: Umfang berechnen
Schauen wir uns das obere Beispiel an. Es soll nun der Umfang bestimmt werden:
Um den Umfang zu bestimmen, starten wir an einem Punkt und gehen dann einmal um die Fläche herum, bis wir wieder an dem Punkt angekommen sind.
Starten wir unten links in der Ecke:
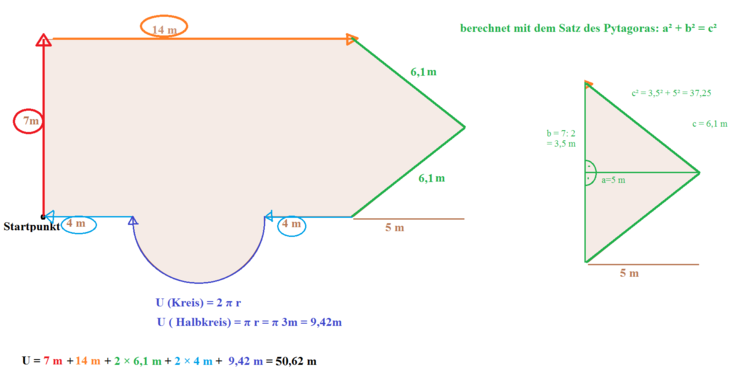
Wir haben uns zwei Beispielaufgaben angeschaut. Um noch weiter zu lernen, kannst du die Übungsaufgaben bearbeiten. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Übungsaufgaben
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
