Ankreis eines Dreiecks konstruieren - Schritt für Schritt erklärt
Neben dem Umkreis und dem Inkreis existiert noch ein weiterer besonderer Kreis, der bei Dreiecken wichtig ist - der Ankreis. Jedes Dreieck besitzt drei Ankreise. Ein Ankreis berührt jeweils eine Dreiecksseite von außen und die Verlängerungen der beiden anderen Seiten. Schauen wir uns nun Schritt für Schritt an, wie wir die drei Ankreise eines Dreiecks konstruieren können.
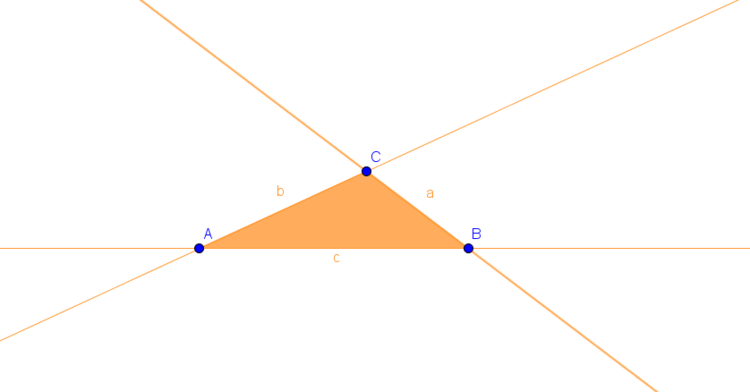
1. Schritt: Dreiecksseiten verlängern
Um einen Ankreis zu konstruieren, müssen wir zunächst die drei Seiten des Dreiecks in beide Richtungen verlängern,
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
2. Schritt: Mittelpunkt einzeichnen
Als nächstes müssen wir den Mittelpunkt des Ankreises einzeichnen. Dazu konstruieren wir zunächst die Winkelhalbierende zwischen der Seite, die der Ankreis berühren soll und den verlängerten Seiten. In unserem Beispiel beginnen wir mit dem Ankreis an der Seite $a$. Somit benötigen wir die Winkelhalbierenden der Verlängerungen der Seiten $b$ und $c$ und der Seite $a$.
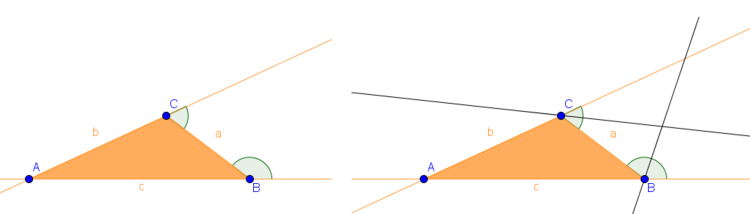
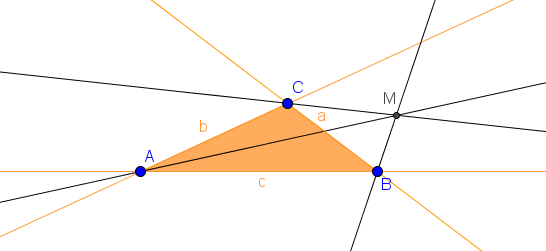
Außerdem müssen wir nun noch die Winkelhalbierende im gegenüberliegenden Punkt einzeichnen. In unserem Fall also am Punkt $A$. Der Schnittpunkt aller drei Winkelhalbierenden ist der Mittelpunkt des Ankreises.
Gut zu wissen
Theoretisch würde es genügen, die ersten beiden Winkelhalbierenden einzuzeichnen. Schon der Schnittpunkt dieser beiden Halbgeraden entspricht dem Mittelpunkt. Allerdings empfiehlt es sich, die dritte Winkelhalbierende ebenfalls zu zeichnen, um zu überprüfen, ob man zuvor richtig gearbeitet hat.
3. Schritt: Radius bestimmen und Ankreis zeichnen
Um den Ankreis zeichnen zu können, benötigen wir nun noch den Radius. Dazu setzen wir den Zirkel so an, dass er die Seite $a$ berührt (tangiert).
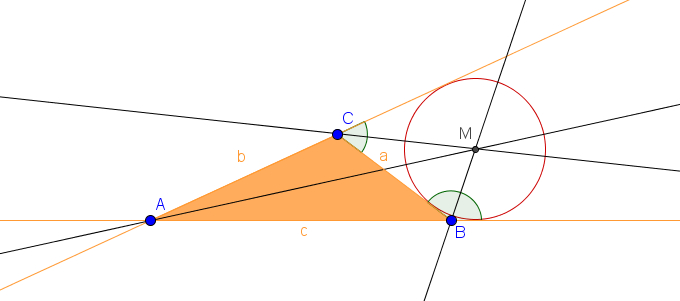
Auf dieselbe Art und Weise konstruieren wir nun noch die Ankreise für die Seiten $b$ und $c$. In der folgenden Abbildung siehst du alle drei Ankreise. Der Ankreis an der Seite $c$ ist sehr groß, weshalb er nicht ganz dargestellt wird.
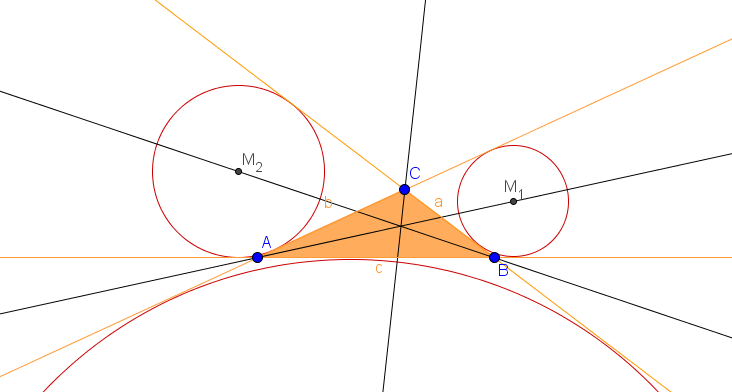
Methode
Vorgehensweise beim Konstruieren eines Ankreises
1. Dreiecksseiten verlängern
2. Mittelpunkt einzeichnen
3. Radius bestimmen und Ankreis zeichnen
Diese Schritte musst du für jede Dreiecksseite wiederholen. Am Ende musst du für jedes Dreieck drei Ankreise eingezeichnet haben.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
