Quadratische Ungleichungen lösen - einfach erklärt

$2x^2+3x-5$

1. Relationszeichen durch ein Gleichheitszeichen ersetzen.

$2x^2+3x-5 = 0$

2. Die Gleichung lösen.

$2x^2+3x -5 = 0~~~~~~~~~~|:2$

$x^2+1,5x -2,5 = 0$

Diese Gleichung können wir nun mit der p-q-Formel lösen.

$x_{1/2} = -\frac{1,5}{2}\pm \sqrt{(\frac{1,5}{2})^2 +2,5}$

$x_{1/2} = -0,75\pm 1,75$

$x_1 = 1$

$x_2 = - 2,5$

Mithilfe der Lösung der Gleichung ermitteln wir nun die Lösung für die Ungleichung.

Wenn wir für $x$ die Zahl $1$ oder $-2,5$ einsetzen, ist das Ergebnis der Gleichung null. Wenn wir die Ungleichung lösen wollen, suchen wir jedoch nach denjenigen Zahlen, die wir für $x$ einsetzen können, damit das Ergebnis des quadratischen Terms kleiner als null ist. Entweder sind dies die Zahlen, die zwischen den beiden Nullstellen liegen, oder die Zahlen, die außerhalb der beiden Nullstellen liegen. Welcher der beiden Zahlenbereiche die Ungleichung löst, ermitteln wir durch Ausprobieren:

Wir setzten zunächst eine Zahl, die zwischen $-2,5$ und $1$ liegt, in die Gleichung ein. Wir nehmen den Wert $0$, da dies einfach zu rechnen ist:

$ x= 0$

$2\cdot 0^2+3\cdot 0-5 = -5 $

$-5$

Das heißt, alle Zahlen, die zwischen den Werten $-2,5$ und $1$ liegen, lösen die Ungleichung. Dies müssen wir nun noch mathematisch ausdrücken:

$2x^2+3x-5$

$L = {x| -2,5}$

Dabei steht das $L$ für Lösungsmenge. Die Lösungsmenge besteht aus allen Zahlen, die größer als $-2,5$ und kleiner als $1$ sind.

Wir können dies mit dem Graphen der quadratischen Funktion überprüfen:

Abbildung: $f(x) = 2x^2 + 3x -5$

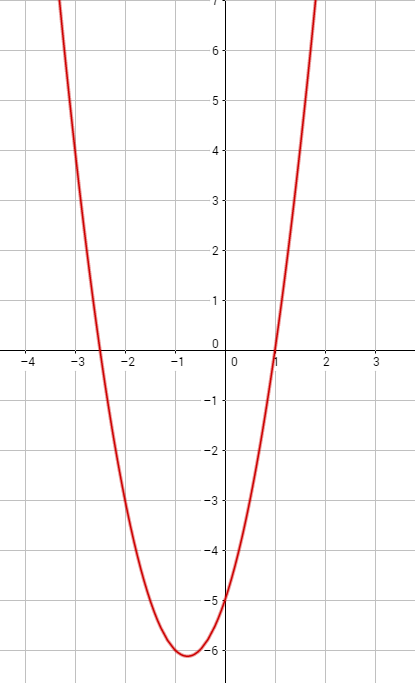
Wir sehen, dass die Nullstellen bei $-2,5$ und $1$ liegen. Wir sehen auch, dass die Funktionswerte (y-Werte) aller Zahlen, die zwischen den beiden Nullstellen liegen, negativ sind; die Punkte liegen unterhalb der x-Achse. Wir haben unsere Rechnung nun graphisch überprüft. 

$-2x^2 +3 \ge 1$

Zuerst lösen wir die Ungleichung graphisch, indem wir den Graphen der quadratischen Funktion zeichnen.

Abbildung: $f(x)=-2x^2 +3$

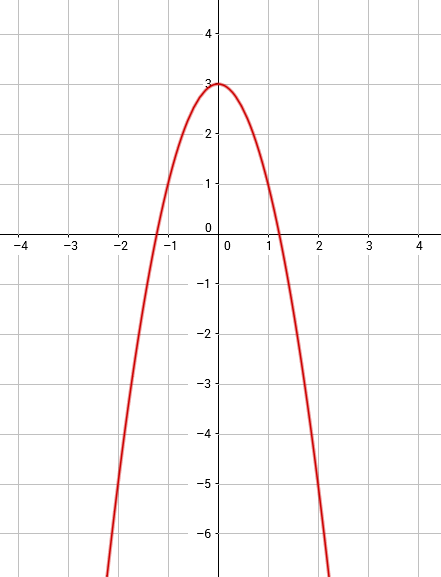
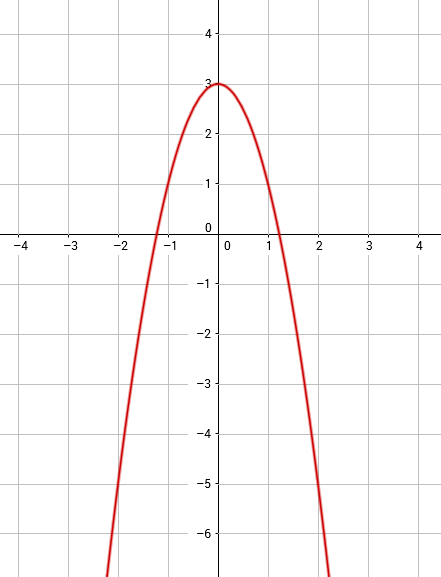
Die quadratische Ungleichung fragt danach, für welche x-Werte die Funktionswerte (y-Werte) größer gleich $1$ sind. Schauen wir uns die Abbildung an, erkennen wir, dass für alle x-Werte die zwischen $-1$ und $1$ liegen, die y-Werte größer als $1$ sind. Da hier das Relationszeichen größer gleich ist, sind $-1$ und $1$ in der Lösungsmenge enthalten.

$L = {x| -1 \le x \le 1}$

Nun kontrollieren wir das Ergebnis mit dem rechnerischen Lösungsweg:

1. Das Relationszeichen durch ein Gleichheitszeichen ersetzen:

$-2x^2 +3 = 1$

2. Die Gleichung lösen.

$-2x^2+3 = 1~~~~~~~~~|-3$

$-2x^2 = -2~~~~~~~~~~~~|:-2$

$x^2 = 1~~~~~~~~~~~~~~~~~~~~| \pm\sqrt{~}$

$x_1 = 1$

$x_2 = -1$

3. Ausprobieren

Außerhalb der beiden Nullstellen: 

$x = 2$    in    $-2x^2 +3 \ge 1$

$-2\cdot2^2 +3 \ge 1$

$-8+3 \ge 1$

$-5 \ge 1~~~~~\textcolor{red}{falsch}$

Zwischen den beiden Nullstellen:

$x=0,5$    in    $-2x^2 +3 \ge 1$

$-2\cdot 0,5^2+3 \ge 1$

$-0,5+3 \ge 1$

$2,5 \ge 1~~~~~\textcolor{red}{richtig}$

Damit liegen die gesuchten x-Werte zwischen den beiden Nullstellen. Da wir bei dieser Aufgabe das größer gleich Zeichen gegeben haben, gehören die Intervallgrenzen (Randwerte) auch zur Lösungsmenge:

$L = {x| -1 \le x \le 1}$