Lineare Gleichungssysteme lösen - Einsetzungsverfahren
Lineare Gleichungssysteme lassen sich auf viele Arten lösen. Für den Fall, dass wir ein Gleichungssystem betrachten, das aus zwei Gleichungen besteht, bietet sich das sogenannte Einsetzverfahren an. Bei Gleichungssystemen mit mehr Gleichungen und Variablen ist diese Methode meist zu aufwendig.
Merke
Merke
Beim Einsetzverfahren löst man eine der beiden Gleichungen nach einer Variablen auf und setzt diese in die andere Gleichung ein.
Beispiel
Beispiel
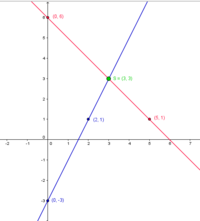
Betrachten wir dieses lineare Gleichungssystem:
$|6\cdot x + 12 \cdot y = 30|$
$|3 \cdot x + 3\cdot y = 9|$
1. Schritt: Eine Gleichung nach einer Variablen auflösen
Für den ersten Schritt musst du zunächst eine Entscheidung treffen: Welche Gleichung willst du nach welcher Variablen umformen? Theoretisch ist es egal wofür du dich entscheidest, da alles zum selben Ergebnis führt. Du wirst später aber auch auf Aufgaben stoßen, bei der ein Weg durchaus schwerer sein kann als der andere. Manchmal muss man also einfach ausprobieren, welcher Weg sich als der bessere erweist.
In unserem Beispiel beginnen wir mit der oberen Gleichung und stellen nach der Variablen $x$ um. Diese Umformung folgt den Regeln zum Lösen von Gleichungen. Dein wichtigstes Werkzeug ist also die Äquivalenzumformung.
$6\cdot x + 12 \cdot y = 30~~~~| -12\cdot y$
$6 \cdot x = 30 - 12\cdot y~~~~| : 6$
$x = 5 - 2 \cdot y$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
2. Schritt: Ausdruck der Variable in die andere Gleichung einsetzen
Den Ausdruck, den wir für $x$ erhalten haben, können wir nun in die zweite Gleichung einsetzen.
$3 \cdot x + 3\cdot y = 9~~~~| $x einsetzen
$3 \cdot (5 - 2\cdot y) + 3\cdot y = 9$
Durch das Einsetzen von $x$ erhalten wir eine Gleichung, die nur eine Variable, in diesem Fall $y$, enthält. Durch Umformen erhalten wir einen exakten Wert für $y$:
$3 \cdot (5 - 2\cdot y) + 3\cdot y = 9~~~~| $Klammer ausmultiplizieren
$15 - 6\cdot y + 3\cdot y = 9~~~~|$zusammenfassen
$15 - 3\cdot y = 9~~~~| -15$
$- 3\cdot y = - 6~~~~| : (-3)$
$y = 2$
3. Schritt: Ausgerechnete Variable einsetzen
Wir haben einen Wert für $y$. Nun müssen wir diesen Wert noch in eine der beiden Ausgangsgleichungen einsetzen, die ja sowohl die Variable $x$ als auch die Variable $y$ enthalten. Welche Gleichung du nimmst ist egal.
Wir setzen den errechneten Wert für $y$ in die erste Gleichung ein.
$6\cdot x + 12 \cdot y = 30~~~~| $y einsetzen
$6\cdot x + 12 \cdot 2 = 30~~~~| $umformen
$6 \cdot x + 24 = 30~~~~| - 24$
$6 \cdot x =6~~~~|:6$
$x = 1$
Wir erhalten als Lösung also $x = 1$ und $y = 2$.
4. Probe der Ergebnisse
Um sicher zu gehen, dass die Ergebnisse korrekt sind, setzen wir zum Schluss noch die errechneten Werte für $x$ und $y$ in die beiden Gleichungen ein.
$6\cdot 1 + 12 \cdot 2 = 30~~~~~~~~~~3\cdot 1 + 3\cdot 2 = 9$
$30 = 30~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~9 = 9$
Der mathematische Ausdruck ist korrekt, somit ist unsere Lösung richtig.
Merke
Merke
Lösen von linearen Gleichungen mit Hilfe des Einsetzverfahrens
1. Eine Gleichung nach einer Variablen auflösen.
2. Ausdruck der Variable in die andere Gleichung einsetzen.
3. Ausgerechnete Variable einsetzen.
4. Probe der Ergebnisse mit Hilfe der Ausgangsgleichungen.
Jetzt hast du einen detaillierten Überblick über die Anwendung des Einsetzungsverfahren zur Lösung von linearen Gleichungssystemen bekommen. Ob du alles verstanden hast, kannst du nun anhand unserer Übungen testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
