2. binomische Formel: Herleitung und Beispiele
In diesem Lerntext beschäftigen wir uns mit der zweiten binomischen Formel. Die zweite binomische Formel hilft dir beim Auflösen von Differenzen zum Quadrat.
Merke
Merke
2. binomische Formel
$(\textcolor{blue}{a} \textcolor{green}{-} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2$
Rechnerische Herleitung der zweiten binomischen Formel
Die Herleitung der zweiten binomischen Formel folgt den Regeln des Auflösens von Klammern und ist leicht nachvollziehbar. Zunächst müssen wir die Potenz ausschreiben:
$(a - b)^2 = (a - b) \cdot (a - b)$
Nun können beide Klammer ausmultipliziert werden. Dabei müssen wir vor allem auf die negativen Vorzeichen achten.
$(a - b) \cdot (a - b) = a^2 + (a \cdot (-b)) + (-b \cdot a) + b^2 $
Die beiden mittleren Klammern haben den gleichen mathematischen Ausdruck und lassen sich zusammenfassen.
$a^2 + (a \cdot (-b)) + (-b \cdot a) + b^2= a^2 - 2\cdot a \cdot b + b^2$
Wir erhalten die zweite binomische Formel. Die erste und zweite binomische Formel unterscheiden sich also nur im Plus- und Minuszeichen in der Klammer. Ihre Herleitungen ähneln sich sehr.
Merke
Merke
2. binomische Formel
$(\textcolor{blue}{a} \textcolor{green}{-} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele für die zweite binomische Formel
Beispiel
Beispiel
- $(\textcolor{blue}{a} \textcolor{green}{-} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2$
- $(\textcolor{blue}{5} \textcolor{green}{-} \textcolor{red}{b})^2 = \textcolor{blue}{5}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{5} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2 = 25 - 10 \cdot b + b^2 $
- $(\textcolor{blue}{a} \textcolor{green}{-} \textcolor{red}{9})^2 = \textcolor{blue}{a}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{9} +\textcolor{red}{9}^2 = a^2 - 18 \cdot a + 81$
- $(\textcolor{blue}{2\cdot z} \textcolor{green}{-} \textcolor{red}{y})^2 = \textcolor{blue}{4\cdot z}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{2\cdot z} \cdot \textcolor{red}{y} +\textcolor{red}{y}^2 = 4 \cdot z^2 - 4 \cdot z \cdot y + y^2$
Grafische Herleitung der zweiten binomischen Formel
Da die binomischen Formeln einen quadratischen Ausdruck beschreiben, lässt sich die zweite binomische Formel auch grafisch mit Hilfe des Flächeninhalts herleiten.
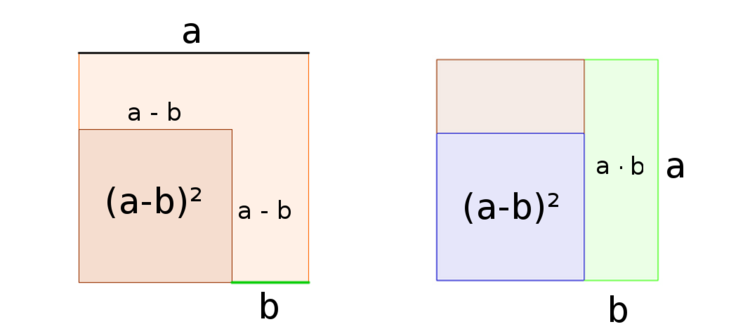
Betrachten wir zunächst das linke Quadrat: Das äußere Quadrat mit der Seitenlänge $a$ hat den Flächeninhalt $a^2$. Das innere Quadrat mit den Seitenlängen $a - b$ besitzt den Flächeninhalt $A = (a - b)^2$
Die rechte Abbildung zeigt, dass man das Quadrat auch in ein inneres Rechteck mit dem Flächeninhalt $A = a\cdot b$ zerlegen kann. Tatsächlich können wir zwei Rechtecke mit diesem Flächeninhalt einzeichnen, die sich dann jedoch überschneiden. Das Quadrat, was sich durch die Überschneidung ergibt, entspricht dem Flächeninhalt $b^2$.
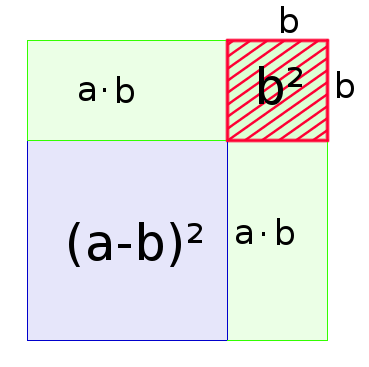
Um nun den Flächeninhalt des inneren, blauen Rechtecks ($(a-b)^2$) zu berechnen, müssen wir die zwei Rechtecke mit dem Flächeninhalt $a \cdot b$ vom Flächeninhalt des gesamten Quadrats abziehen ($a^2$).
$(a-b)^2 = a^2 - 2 \cdot a \cdot b$
Allerdings überschneiden sich die beiden grünen Rechtecke. Der Flächeninhalt des Quadrates, das durch diese Überschneidung entsteht ($b^2$), muss also wieder dazu gerechnet werden. Dadurch erhalten wir die zweite binomische Formel:
$(a-b)^2 = a^2 - 2 \cdot a \cdot b + b^2$
Dein neu erlerntes Wissen kannst du nun mit unseren Übungsaufgaben testen! Viel Spaß dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
