3. binomische Formel: Herleitung und Beispiele
In diesem Lerntext beschäftigen wir uns mit der dritten binomischen Formel. Die dritte binomische Formel hilft dir beim Zusammenfassen zweier Klammern, die miteinander multipliziert werden und die gleichen Variablen besitzen. Die jeweils zweite Variable hat jedoch ein anderes Vorzeichen.
Merke
3. binomische Formel
$(\textcolor{blue}{a} + \textcolor{red}{b}) \cdot (\textcolor{blue}{a} - \textcolor{red}{b}) = (\textcolor{blue}{a}^2 - \textcolor{red}{b}^2)$
Rechnerische Herleitung der dritten binomischen Formel
Die Herleitung der dritten binomischen Formel folgt, ähnlich wie bei der ersten und zweiten binomischen Formel, ganz normalen Umformungsregeln. Zunächst multiplizieren wir die Klammern miteinander, indem wir jede Variable innerhalb der einen Klammer mit den Variablen der anderen Klammer multiplizieren.
$(a + b) \cdot (a - b) = a \cdot a + a \cdot ( - b) + b\cdot a + b \cdot (- b)$
Rechnen wir die Vorzeichen zusammen erhalten wir folgenden Term:
$a \cdot a + a \cdot ( - b) + b\cdot a + b \cdot (- b) = a^2 - a\cdot b + a \cdot b - b^2$
Die beiden mittleren Ausdrücke ($a\cdot b$ und $-a \cdot b$) kürzen sich gegenseitig raus. Was übrig bleibt ist die dritte binomische Formel:
$a^2 - a\cdot b + a \cdot b - b^2 = a^2 - b^2$
Merke
3. binomische Formel
$(\textcolor{blue}{a} + \textcolor{red}{b}) \cdot (\textcolor{blue}{a} - \textcolor{red}{b}) = (\textcolor{blue}{a}^2 - \textcolor{red}{b}^2)$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele für die dritte binomische Formel
Beispiel
$(\textcolor{blue}{a} + \textcolor{red}{b}) \cdot (\textcolor{blue}{a} - \textcolor{red}{b}) = (\textcolor{blue}{a}^2 - \textcolor{red}{b}^2)$
$(\textcolor{blue}{3} + \textcolor{red}{x}) \cdot (\textcolor{blue}{3} - \textcolor{red}{x}) = (\textcolor{blue}{3}^2 - \textcolor{red}{x}^2) = (9 - x^2)$
$(\textcolor{blue}{a} + \textcolor{red}{5}) \cdot (\textcolor{blue}{a} - \textcolor{red}{5}) = (\textcolor{blue}{a}^2 - \textcolor{red}{5}^2) = (a^2 - 25)$
$(\textcolor{blue}{81} - \textcolor{red}{y}^4) = (\textcolor{blue}{9} + \textcolor{red}{y^2}) \cdot (\textcolor{blue}{9} - \textcolor{red}{y^2})$
Geometrische Herleitung der dritten binomischen Formeln
Ähnlich wie die erste und die zweite binomische Formel lässt sich auch die dritte binomische Formel grafisch über die Flächeninhalte von Rechtecken herleiten bzw. beweisen.
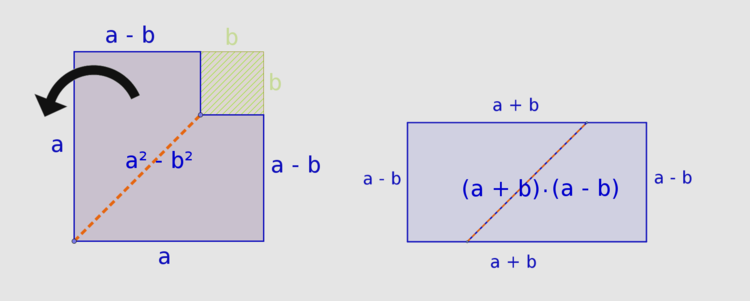
In der linken Abbildung entspricht das blaue Vieleck dem Flächeninhalt $A_{Vieleck} = a^2 - b^2$. Dasselbe Vieleck lässt sich an der Diagonalen auseinander schneiden und ergibt neu zusammengesetzt ein Rechteck mit dem Flächeninhalt $A_{Rechteck}= (a+b) \cdot (a-b)$, das du in der rechten Abbildung siehst.
Da der Flächeninhalt durch die Transformation nicht geändert wurde, kann man die unterschiedlichen Ausdrücke gleichsetzen:
$A_{Vieleck} = A_{Rechteck}$
$a^2 - b^2 = (a + b) \cdot (a - b)$
Wir erhalten auch hier die dritte binomische Formel.
Anwendung der dritten binomischen Formel
Die dritte binomische Formel kann genutzt werden, um Produkte der folgenden Art zu vereinfachen und gegebenenfalls ohne Taschenrechner auszurechnen:
$105 \cdot 95 = (100 + 5) \cdot (100 - 5) = 100^2 - 5^2 = 10000 - 25 = 9975$
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Berechne das Ergebnis mit Hilfe der dritten binomischen Formel. Benutze keinen Taschenrechner!
$6^2 - 5^2$
Wie lässt sich der Term mit Hilfe der dritten binomischen Formel vereinfachen?
$(x + 5) \cdot (x - 5)$
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
