1. binomische Formel: Herleitung und Beispiele
Die erste binomische Formel hilft dir beim Auflösen von Summen aus zwei Summanden zum Quadrat.
Merke
1. binomische Formel
$(a + b)^2 = a^2 + 2 \cdot a \cdot b + b^2$
Rechnerische Herleitung der ersten binomischen Formel
Die binomischen Formeln leiten sich aus den Regeln zum Auflösen von Klammern ab. Für die Herleitung genügt es also den Term ohne Kenntnis der binomischen Formel aufzulösen.
Zunächst schreiben wir die Potenz aus:
$(a + b)^2 = (a + b) \cdot (a + b)$
Nun können wir die beiden Klammern ausmultiplizieren:
$(a + b) \cdot (a + b) = (a \cdot a) + (a \cdot b) + (b \cdot a) + (b \cdot b) = a^2 + (a \cdot b) + (b \cdot a) + b^2$
Die beiden mittleren Klammern haben den gleichen mathematischen Ausdruck und lassen sich zusammenfassen.
$a^2 + (a \cdot b) + (b \cdot a) + b^2 = a^2 + (a \cdot b) + (a \cdot b) + b^2 = a^2 + 2 \cdot a \cdot b + b^2$
Wir erhalten die erste binomische Formel.
Merke
1. binomische Formel
$(\textcolor{blue}{a} \textcolor{green}{+} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{+} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} + \textcolor{red}{b}^2$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele für die erste binomische Formel
Beispiel
- $(\textcolor{blue}{a} \textcolor{green}{+} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{+} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2$
- $(\textcolor{blue}{7} \textcolor{green}{+} \textcolor{red}{h})^2 = \textcolor{blue}{7}^2 \textcolor{green}{+} 2 \cdot \textcolor{blue}{7} \cdot \textcolor{red}{h} +\textcolor{red}{h}^2 = 49 + 14\cdot h + h^2$
- $(\textcolor{blue}{x} \textcolor{green}{+} \textcolor{red}{9})^2 = \textcolor{blue}{x}^2 \textcolor{green}{+} 2 \cdot \textcolor{blue}{x} \cdot \textcolor{red}{9} +\textcolor{red}{9}^2 = x^2 + 18 \cdot x + 81$
- $(\textcolor{blue}{2 \cdot x} \textcolor{green}{+} \textcolor{red}{y})^2 = \textcolor{blue}{4 \cdot x}^2 \textcolor{green}{+} 2 \cdot \textcolor{blue}{2\cdot x} \cdot \textcolor{red}{y} +\textcolor{red}{y}^2 = 4 \cdot x^2 + 4 \cdot x \cdot y + y^2$
Grafische Herleitung der ersten binomischen Formel
Da die binomischen Formeln einen quadratischen Ausdruck beschreiben, lässt sich die erste binomische Formel auch grafisch, mit Hilfe des Flächeninhalts, herleiten.
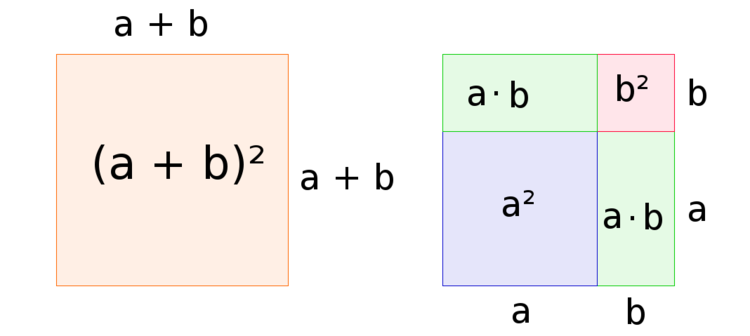
Die Flächeninhalte der Quadrate sind gleich groß, werden aber unterschiedlich errechnet. Der Flächeninhalt des linken Quadrats ergibt sich aus der Multiplikation der Seitenlängen:
$A_{links} = (a + b) \cdot (a + b) = (a + b)^2$
Im rechten Quadrat rechnen wir den Flächeninhalt aus, indem wir die Flächeninhalte kleinerer Flächen addieren. Wir zerlegen das große Quadrat in ein kleineres Quadrat mit den Seitenlängen $a$, ein weiteres kleines Quadrat mit den Seitenlängen $b$ und zwei Rechtecke mit den Seitenlängen $a$ und $b$. Daraus ergeben sich folgende Flächeninhalte:
- $A_{1} = a^2$
- $A_{2} = b^2$
- $A_{3} = a \cdot b$
Rechnen wir die Flächeninhalte des rechten Quadrats nun zusammen und beachten dabei, dass das innere Rechteck mit den Seitenlängen $a$ und $b$ zweimal vorkommt, erhalten wir folgenden Gesamtausdruck:
$A_{rechts}= a^2 + 2\cdot a\cdot b + b^2$
Da der Flächeninhalt des rechten gleich dem des linken Quadrates ist, gilt:
$A_{links} =A_{rechts}$
$ (a+b)^2 = a^2 + 2\cdot a\cdot b + b^2$
Wir erhalten die erste binomische Formel.
Nun hast du einen Überblick darüber erhalten, wie die erste binomische Formel gebildet wird. Schau zur Vertiefung auch in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Wie lässt sich der Term mit Hilfe der ersten binomischen Formel umformen?
$(y^2 + x)^2$
Wie lässt sich der Term mit Hilfe der ersten binomischen Formel umformen?
$(x + 10)^2$
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
