Pq Formel - Aufgaben und Herleitung

Herleitung der pq Formel

Um von der Normalform auf die p-q-Formel zu kommen, wird die quadratische Gleichung mit Hilfe von Äquivalenzumformungen, der quadratischen Ergänzung und den binomischen Formeln nach $x$ umgestellt.

$x^2 + \textcolor{red}{p} \cdot x + \textcolor{orange}{q} = 0  | -\textcolor{orange}{q}$

$x^2 + \textcolor{red}{p} \cdot x = - \textcolor{orange}{q}$ | $+ (\frac{ \textcolor{red}{p}}{2})^2 $ (quadratische Ergänzung)

$x^2 + \textcolor{red}{p} \cdot x + (\frac{ \textcolor{red}{p}}{2})^2 = (\frac{ \textcolor{red}{p}}{2})^2 - \textcolor{orange}{q}$

Um mit dem Term weiterzurechnen, müssen wir die linke Seite so umschreiben, dass wir dort die 1. binomische Formel anwenden können.

$x^2 + \textcolor{red}{p} \cdot x + (\frac{ \textcolor{red}{p}}{2})^2 = (\frac{ \textcolor{red}{p}}{2})^2 - \textcolor{orange}{q}$ | Umformung

$x^2 + 2\cdot (\frac{\textcolor{red}{p}}{2}) \cdot x + (\frac{ \textcolor{red}{p}}{2})^2 = (\frac{ \textcolor{red}{p}}{2})^2 - \textcolor{orange}{q}$ | Anwendung der ersten binomischen Formel

$ (x + \frac{\textcolor{red}{p}}{2})^2 = (\frac{\textcolor{red}{p}}{2})^2 - \textcolor{orange}{q} | \pm \sqrt{}$

$x + \frac{\textcolor{red}{p}}{2} = \pm \sqrt{(\frac{\textcolor{red}{p}}{2})^2 - \textcolor{orange}{q}} | -\frac{\textcolor{red}{p}}{2}$

$x = -\frac{\textcolor{red}{p}}{2}\pm \sqrt{(\frac{\textcolor{red}{p}}{2})^2-\textcolor{orange}{q}}$

Pq Formel Übung mit Lösung

Betrachten wir folgende quadratische Gleichung:

$3 \cdot x^2 - 6\cdot x - 24 = 0$

Die Gleichung liegt nicht in der Normalform vor. Wir müssen also zunächst durch den Faktor, der vor dem $x^2$ steht, teilen.

$3 \cdot x^2 - 6\cdot x - 24 = 0$   | $:3$

$x^2 - 2\cdot x - 8 = 0$

Die quadratische Gleichung liegt nun in der Normalform vor und wir können die p-q-Formel anwenden.

$x^2 + \textcolor{red}{p} \cdot x + \textcolor{orange}{q} = 0$ $~~~~~~~~~~~~~~~~\rightarrow$   $x^2 \textcolor{red}{-2}\cdot x \textcolor{orange}{-8} = 0$

$x_{1/2} = -\frac{\textcolor{red}{p}}{2}\pm \sqrt{(\frac{\textcolor{red}{p}}{2})^2-\textcolor{orange}{q}}$  $~~~~~~~~\rightarrow$  $x_{1/2} = -\frac{\textcolor{red}{-2}}{2}\pm \sqrt{(\frac{\textcolor{red}{-2}}{2})^2-\textcolor{orange}{-8}}$

Wir erhalten für $x$ folgende Werte:

$x_1 = - 2~~~~~~~~~x_2 = 4$

Pq Formel: Lösungen

Eine quadratische Gleichung kann unterschiedlich viele Lösungen haben. Man unterscheidet zwischen:

• zwei reellen Lösungen

• einer reellen Lösung

• keiner Lösung

Wie viele Lösungen die quadratische Gleichung hat, hängt von dem Term unterhalb der Wurzel in der p-q-Formel ab.

Schauen wir uns nun die drei Fälle der Diskriminanten an. Wir geben dir zu den Lösungsarten der pq Formel Beispiele an die Hand, damit du dir dieses neue Wissen leichter einprägen kannst:  

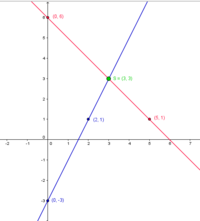
Pq Formel: 1. Die Diskriminante ist größer als null ($D~>~0$)

Ist die Diskriminante größer als null, ergibt die p-q-Formel zwei reelle Zahlen als Lösung.

Pq Formel: 2. Die Diskriminante ist gleich null ($D = 0$)

Wenn die Diskriminante null ist, erhalten wir nur eine reelle Lösung.

Pq Formel: 3. Die Diskriminante ist kleiner als null ($D~<~0$)

Wenn die Diskriminante kleiner als null ist, ist der Wert unterhalb der Wurzel eine negative Zahl. Die Wurzel von negativen Zahlen zu errechnen ist mathematisch jedoch nicht möglich. Die quadratische Gleichung besitzt dann keine reelle Lösung.

Jetzt kennst du die pq Formel Erklärung, Herleitung und Anwendung. Dein neu erlerntes Wissen kannst du nun noch an unseren Aufgaben zur pq Formel testen! Viel Erfolg dabei!