Pascalsches Dreieck und binomische Formeln
In diesem Lerntext geben wir dir zu dem sogenannten Pascalschen Dreieck eine Erklärung. Das Pascalsche Dreieck ist eine bestimmte Anordnung von Zahlen, die auf den ersten Blick ein wenig ungewöhnlich aussieht. Tatsächlich sind diese Zahlen allerdings nach einem ganz bestimmten System geordnet und helfen uns darüber hinaus auch noch beim Rechnen und Aufstellen binomischer Formeln höheren Grades. Am Ende dieses Lerntextes findest du zum Thema Pascalsches Dreieck Übungen, um dein erlerntes Wissen zum Pascalschen Dreieck in der Anwendung zu vertiefen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Pascalsches Dreieck: Form und Aussehen
Wie der Name bereits verrät, erscheint die Zahlenfolge eines Pascalschen Dreiecks in einer dreieckigen Form. Diese ergibt sich daraus, dass die Zeilen von oben nach unten gesehen immer länger werden. Die erste Zahlenreihe besteht nur aus einer einzelnen Zahl: der Eins. Pro Zeile kommt nun eine weitere Zahl zur Zahlenreihe hinzu, dabei stehen am Anfang und am Ende jeder Zeile jeweils Einsen. Die Zahlen, die zwischen den Einsen stehen, werden nach einem bestimmten System gebildet. Sie ergeben sich aus der Addition der beiden oberen Zahlen (s. Abbildung).
Das Pascalsche Dreieck lässt sich beliebig oft um weitere Zahlenreihen verlängern, es gibt theoretisch kein Ende.
Beispiel
Pascalsche Dreieck - Anwendung
Setze im Pascalschen Dreieck die fehlenden drei Zahlen ein.
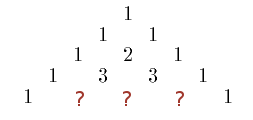
Wir wissen, dass die Zahlen sich aus den Summen der beiden Zahlen ergeben, die links und rechts über dem Fragezeichen stehen. Wir rechnen für die fehlenden Zahlen also:
1. $3 + 1 = 4$
2. $3 + 3 = 6$
3. $3 + 1 = 4$
Pascalsches Dreieck und binomische Formeln
Das Pascalsche Dreieck und binomische Formeln stehen im Zusammenhang zueinander: denn das Pascalsche Dreieck hilft uns, Binome der folgenden Form auszumultiplizieren: $(a + b)^n$
Gut zu wissen
Der Exponent $n$ kann auch $3$, $4$ oder $5$ betragen. Im Lerntext Binomische Formeln hoch 3, 4 und 5 erfährst du mehr.
Dabei entspricht $n$ der Nummer der Zeile im Pascalschen Dreieck, wobei man bei der Nummerierung nicht mit $1$, sondern mit $0$ beginnt.
$\textcolor{blue}{0}.~Zeile~~~~~\textcolor{red}{1}~~~~~~(a~+~b)^0 = 1$
$\textcolor{blue}{1}.~Zeile~~~~\textcolor{red}{1}~\textcolor{red}{1}~~~~(a~+~b)^1 = 1\cdot a + 1\cdot b$
$\textcolor{blue}{2}.~Zeile~~\textcolor{red}{1}~\textcolor{red}{2}~\textcolor{red}{1}~~~(a~+~b)^2 = 1\cdot a^2 + 2\cdot a \cdot b + 1\cdot b^2 $
In der zweiten Zeile erkennen wir die erste binomische Formel wieder. Die Koeffizienten der binomischen Formeln kannst du also direkt am Pascalschen Dreieck ablesen. Dies hilft dir vor allem bei Binomen, deren Exponent $n$ größer als $2$ ist.
Teste und überprüfe dein neu erlerntes Wissen zum Pascalschen Dreieck in unseren Übungen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
