Vielecke: Arten und Eigenschaften
In der Geometrie wird dir irgendwann der Begriff Vieleck begegnen. In diesem Kapitel wollen wir uns mit dem Begriff Vieleck befassen und die dazugehörigen Formeln für den Umfang und den Flächeninhalt erklären.
Vieleck - allgemein
Der Begriff Vieleck bezeichnet in der Geometrie jede Form von Figur, welche mehr als 3 verbundene Kanten hat. Das bedeutet, dass selbst Dreiecke und Vierecke, egal wie sie geformt sind, zu den Vielecken zählen.
Merke
Merke
Vielecke sind Figuren mit mindestens drei verbundenen Ecken.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Vielecke: Zwei Klassen
Regelmäßiges Vieleck
Vielecke werden in zwei verschiedene Klassen unterteilt. Als erstes haben wir die regelmäßigen Vielecke, beispielsweise ein regelmäßiges Achteck, auch Oktagon genannt. Ein Beispiel für ein Oktagon ist das STOP-Schild aus dem Straßenverkehr. Diese Figuren lassen sich mithilfe der Geometrie in kleinere Figuren einteilen, sodass wir den Flächeninhalt berechnen können.
Noch einfacher ist das Errechnen des Umfangs bei regelmäßigen Vielecken. Hierbei ist nur die Länge der Außenseiten und die Anzahl der Seiten entscheidend. Wenn diese beiden Größen gegeben sind, dann lautete die Formel:
Merke
Merke
$Umfang \; = \; Anzahl \; Seiten \; \cdot \; Länge\; der\; Seite$
$U \;=\; n \cdot a$
Unregelmäßiges Vieleck
Die zweite Klasse sind die unregelmäßigen Vielecke. Diese zeichnen sich durch keine besonderen Formen aus und es gibt keine allgemeinen Formeln, wie diese Figuren berechnet werden können. Du musst also bei unregelmäßigen Vielecken versuchen, diese selbst in Teilfiguren zu zerlegen, sodass dir bekannte Figuren herauskommen. Schauen wir uns das an der nächsten Figur einmal an:
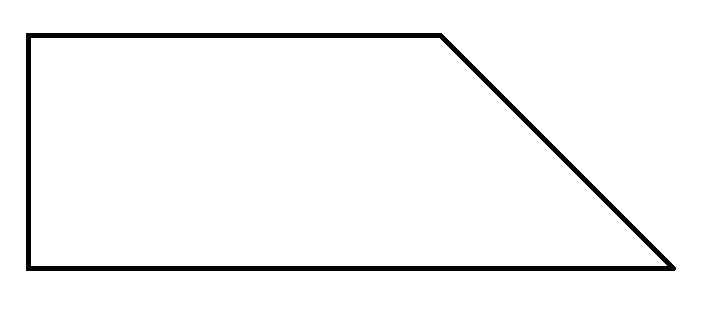
In der Abbildung erkennen wir ein unregelmäßiges Vieleck. Leider gibt es keine Formel, wie wir den Flächeninhalt dieser Figur direkt ausrechnen können. Aber wenn wir die Figur zerteilen, könnten Figuren herauskommen, bei denen wir die Formeln kennen.
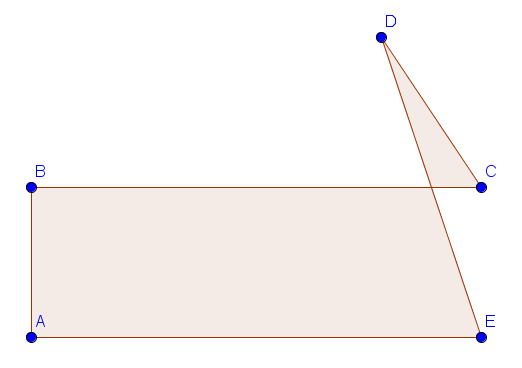
Wir teilen das unregelmäßige Viereck in zwei Figuren: Ein Viereck und ein Dreieck. Dann sieht die Figur so aus:
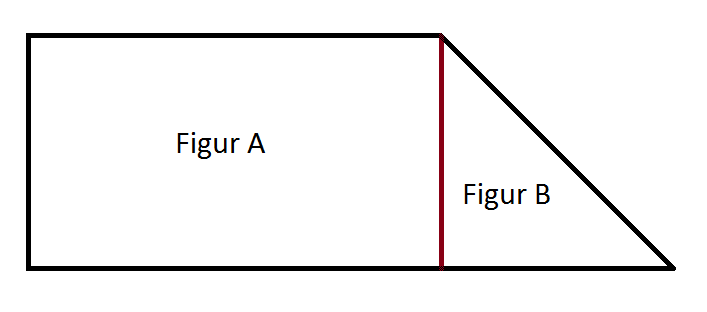
Jetzt werden nur noch die Längen benötigt und wir können den Flächeninhalt und den Umfang errechnen.
Merke
Merke
Es gibt keine allgemeinen Formeln für unregelmäßige Vielecke.
Teile Vielecke in dir bekannte Figuren, damit du den Flächeninhalt und den Umfang errechnen kannst.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dort kannst du dein neues Wissen direkt anwenden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
