Begriffssammlung Mathematik 8. Klasse
In diesem Kapitel kannst du dir einen Überblick über die Themen der 8. Klasse verschaffen. Hierzu zählen unter anderem die Prozentrechnung mit ihren Fachbegriffen, aber auch der Kreis in der Geometrie und die linearen Funktionen. In diesem Lerntext werden die wichtigsten Begriffe noch einmal kurz erklärt. Wenn du mehr zu den einzelnen Themen erfahren möchtest, gelangst du über die verlinkten Überschriften zu den entsprechenden Lerntexten.
Zahlenlehre und Rechengesetze
Prozente
Merke
Prozente drücken Anteile eines Ganzen aus. Ein Prozent entspricht dabei $\frac{1}{100}$ Anteil eines Ganzen.
$x~\% = \frac{x}{100}$
$\textcolor{green}{6~\% = \frac{6}{100}}$
Prozent (von Hundert)
$\% = \frac{1}{100}$
Skala: $0\% - 100 \%$
Grundwert, Prozentwert, Prozentsatz
Merke
Der Grundwert $G$ ist die Basis.
Der Prozentwert $W$ bezeichnet die Zahl, die dem Anteil entspricht.
Die Prozentzahl $p$ ist nichts anderes als die Prozentangabe ohne das Prozentzeichen.
Der Prozentsatz $p\%$ ist die Prozentzahl mit dem $\%$-Zeichen versehen.
Promille
Merke
$‰ = \frac{1}{1000}$
$x~‰ = \frac{x}{1000}$
$\textcolor{green}{6~‰ = \frac{6}{1000}}$
Skala: $0~‰ - 1000~‰$
Zinseszins
Merke
Zinseszins ist der Zins, der auf bereits gutgeschriebene Zinsen bezahlt wird.
Geometrie
Der Kreis
Merke
Der Kreis ist eine geometrische Figur, bei der alle Punkte den gleichen Abstand zum Mittelpunkt haben.
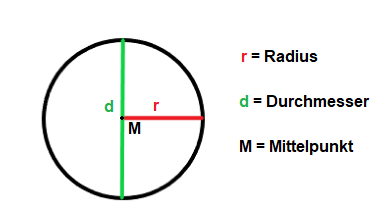
Der Radius ist die Strecke vom Mittelpunkt des Kreises zum Kreisrand.
Der Durchmesser ist die Strecke zwischen zwei Randpunkten, die durch den Mittelpunkt geht.
Für das Verhältnis zwischen Durchmesser und Radius gilt folgender Zusammenhang: $d=2\cdot r$
Kreiszahl Pi
Merke
Die Kreiszahl Pi ist eine mathematische Konstante mit dem Wert:
$\pi = 3,14(1592654.....)$
Geraden, Strecken und Winkel am Kreis
Merke
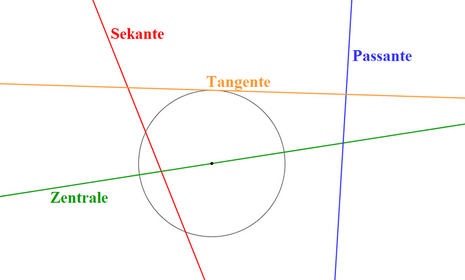
Die Sekante ist eine Gerade, die den Kreis in zwei Punkten schneidet.
Die Passante ist eine Gerade, die am Kreis vorbeigeht, ihn also weder schneidet noch berührt.
Die Tangente ist eine Gerade, die den Kreis in genau einem Punkt berührt.
Die Zentrale ist eine Sekante, die durch den Mittelpunkt verläuft.
Die Sehne ist eine Strecke im Kreis, die zwei Punkte des Kreises verbindet. Wenn die Sehne durch den Mittelpunkt des Kreises geht, wird die Sehne Durchmesser genannt.
Der Vollkreis hat immer $360^\circ$.
Ein Kreisausschnitt ist ein Ausschnitt des Kreises. Der gekrümmte Rand des Kreisausschnittes wird als Kreisbogen bezeichnet.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Funktionen
Die lineare Funktion
Merke
Eine lineare Funktion beschreibt das Verhältnis zweier Variablen.
Allgemeine Form
$f(x) = \textcolor{red}{m}\cdot x + \textcolor{blue}{n}$
$\textcolor{red}{m : Steigung}$
$\textcolor{blue}{n : y-Achsenabschnitt}$
$x :$ unabhängige Variable
$f(x) = y:$ abhängige Variable
Umkehrfunktion
Merke
Um die Umkehrfunktion einer Funktion zu erhalten, musst du die Funktion an der Winkelhalbierenden ($f(x)=x$) spiegeln. Die Umkehrfunktion wird mit $f^{-1}(x)$ gekennzeichnet.
Nullstelle bestimmen
Merke
Die Nullstelle ist der Punkt, an dem die lineare Funktion die x-Achse schneidet.
- die Funktion gleich null setzen
- nach $x$ auflösen
- Nullstelle aufschreiben
Steigungsdreieck einer linearen Funktion
Merke
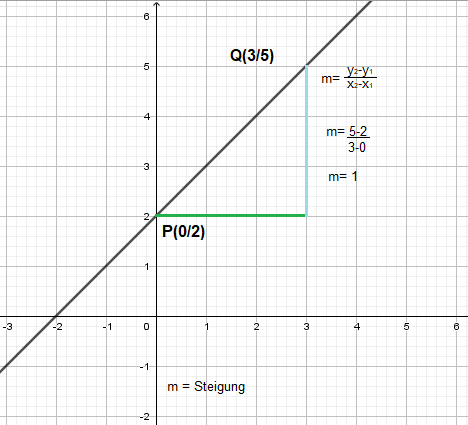
Das Steigungsdreieck ist eine Figur, mit deren Hilfe wir die Steigung einer linearen Funktion ermitteln können.
Vorgehensweise:
1. zwei Punkte, die auf der Funktion liegen, markieren
2. Steigungsdreieck einzeichnen
3. Höhen- und Längenunterschied ermitteln
4. Steigung berechnen, indem der Höhenunterschied durch den Längenunterschied geteilt wird
Schnittwinkel zweier linearer Funktionen
Merke
Wenn sich zwei Geraden schneiden, ergeben sich vier Winkel. Diese nennen wir Schnittwinkel. Die gegenüberliegenden Winkel sind jeweils gleich groß.
Wahrscheinlichkeitsrechnung und Statistik
Spannweite, Varianz und Standardabweichung
Merke
Die Spannweite ist der Abstand zwischen dem kleinsten und dem größten Wert.
Die Varianz ist ein Streuungsmaß. Die Varianz gibt an, ob die Werte wenig oder stark streuen. Je kleiner die Varianz, desto dichter liegen die Werte beieinander.
Die Standardabweichung ist die Wurzel aus der Varianz und wird mit $\sigma$ (Sigma) abgekürzt.
Modus und Median
Merke
Der Modus einer Datenreihe ist der Wert oder auch das Merkmal mit der größten Häufigkeit. Der Modus kann in den meisten Fällen einfach abgelesen werden.
Der Median wird auch Zentralwert genannt und ist der Wert, der in der Mitte einer geordneten Datenreihe steht. Bei einer ungeraden Anzahl an Daten ist der Median der Wert in der Mitte. Bei einer geraden Anzahl an Daten ist der Median der Durchschnitt bzw. das arithmetische Mittel der beiden mittleren Werte.
Arithmetisches Mittel und Durchschnitt
Merke
Das arithmetische Mittel gibt den Durchschnitt einer Datenreihe an. Um es zu berechnen, addierst du alle Zahlen und teilst das Ergebnis durch die Anzahl an Zahlen.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
