Geraden, Strecken und Winkel am Kreis
In diesem Text erklären wir dir, wie verschiedene Geraden und Strecken am Kreis benannt werden und wie die Länge des Kreisbogens berechnet wird.
Geraden am Kreis
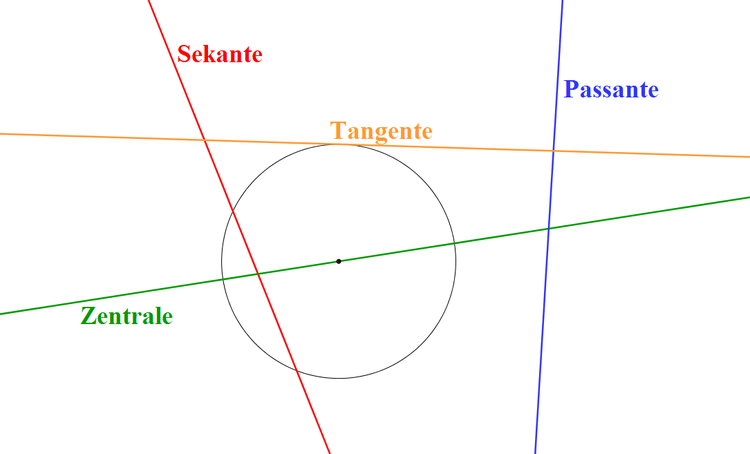
Geraden können in Bezug auf einen Kreis verschieden liegen. Sie können ihn schneiden, an ihm vorbeilaufen oder ihn berühren. Je nach Lage der Gerade wird diese anders bezeichnet. Schauen wir uns dies in der nachfolgenden Abbildung an:
Sekante
Eine Sekante schneidet den Kreis in zwei Punkten.
Zentrale
Eine Zentrale schneidet, wie eine Sekante, den Kreis in zwei Punkten. Doch die Besonderheit einer Zentralen ist es, dass sie durch den Mittelpunkt des Kreises verläuft.
Tangente
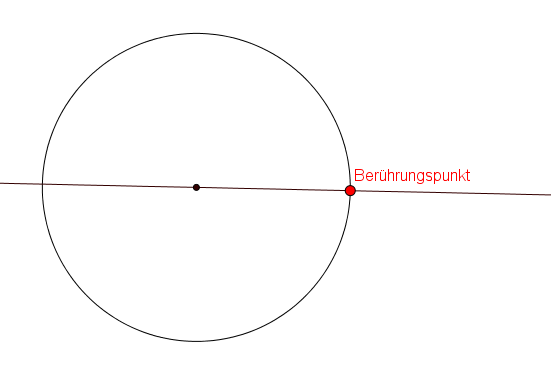
Eine Tangente berührt den Kreis nur an einem Punkt, sie streift den Kreis sozusagen. Den Punkt, an dem sich der Kreis und die Gerade berühren, nennt man Berührungspunkt.
Die Strecke zwischen dem Mittelpunkt und dem Berührungspunkt bildet mit der Tangente einen rechten Winkel.
Beispiel
Beispiel
Konstruktion einer Tangente
1. Den Mittelpunkt und den Berührungspunkt verbinden.
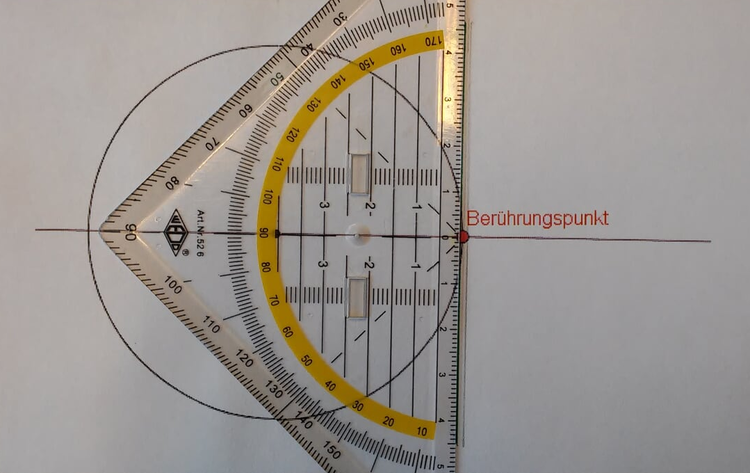
2. Am Berührungspunkt wird nun die Tangente eingezeichnet. Sie muss mit der zuvor eingezeichneten Gerade einen rechten Winkel bilden. Dafür legst du das Geodreieck mit der Mittellinie auf die Gerade. Und zeichnest eine Linie, die durch den Berührungspunkt vorläuft, ein.
Passante
Eine Passante schneidet oder berührt den Kreis nicht.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Unterschied von Gerade und Strecke
Gut zu wissen
Hinweis
Eine Gerade hat kein Ende und keinen Anfang. Sie ist unendlich lang!
Eine Strecke hingegen hat einen Anfang und auch ein Ende. Aus diesem Grund kann die Länge einer Strecke berechnet werden.
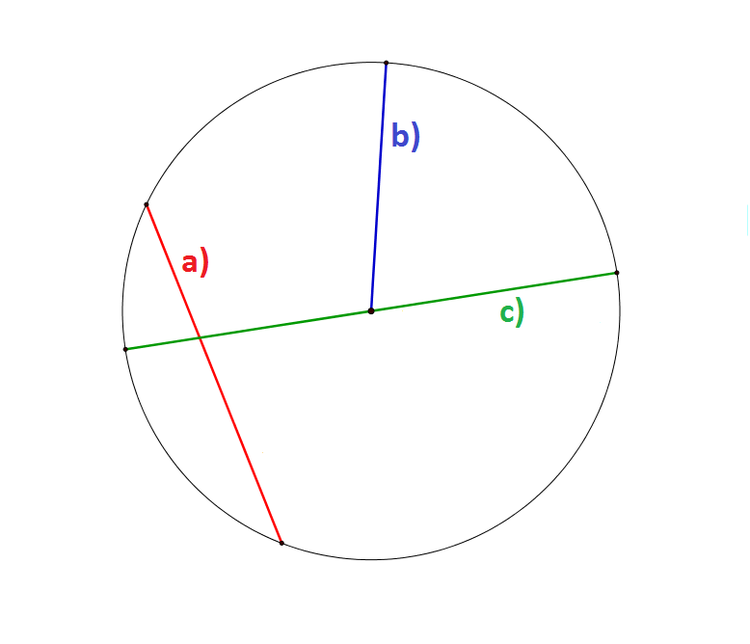
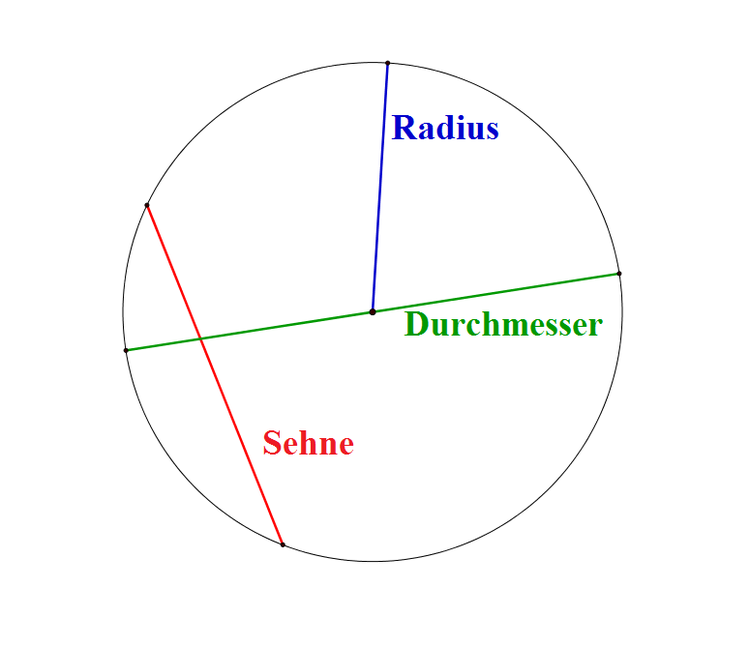
Bezeichnungen von Strecken im Kreis
Auch Strecken werden je nach der Lage im Kreis anderes bezeichnet:
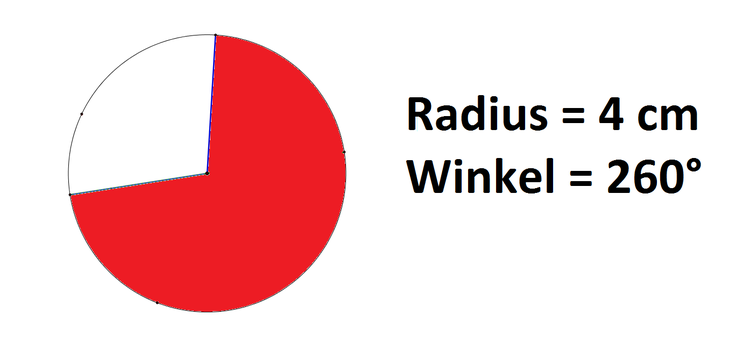
Winkel am Kreis
Um die Größe eines Winkels im Kreis zu messen, sollte zunächst klar sein, dass ein Vollkreis, also eine Drehung einmal herum, $360^\circ$ groß ist. Kreisausschnitte besitzen dann jeweils nur einen Teil des $360^\circ$ großen Winkels. Es wird also nicht einmal ganz herumgedreht, sondern es wird eine Teildrehung betrachtet.
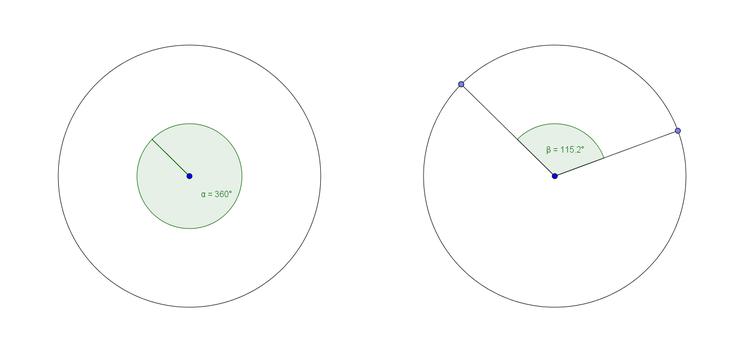
Der Teil des Umfangs von dem Kreisausschnitt wird Kreisbogen genannt.
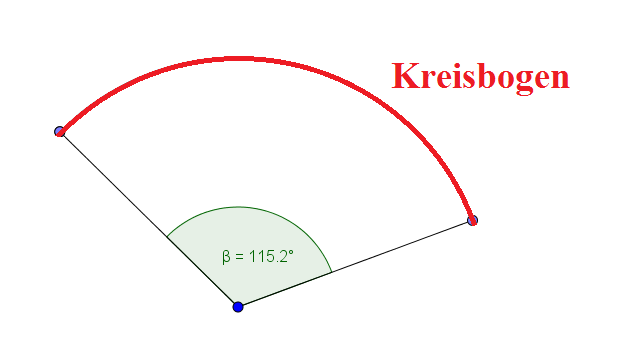
Wie können wir die Länge des Kreisbogens mit der Winkelangabe berechnen. Schauen wir uns dies hier an:
Beispiel
Beispiel
Der Kreisbogen ist ein Teil des Umfangs eines Kreises. Der Umfang wird mit der Formel: $ U = \pi \cdot d$ (d: Durchmesser) berechnet.
Der Winkel $\beta$ ist $115.2^\circ$ groß und der Radius beträgt $5 cm$. Berechnen wir zunächst den Umfang des ganzen Kreises:
$ U = \pi \cdot d = \pi \cdot 2\cdot r = \pi \cdot 10 cm \approx 31,42 cm$ .
Nun brauchen wir den Teil, der $115,2 ^\circ$ groß ist. Um den Anteil des Bogens am Gesamtkreisumfang zu berechnen, müssen wir den Winkel durch $360^\circ$ teilen.
$Anteil = \frac{115,2 ^\circ}{360^\circ}= 0,32$
Nun muss der Anteil mal dem Umfang gerechnet werden und wir erhalten die Länge des Kreisbogens.
$Kreisbogen = 0,32 \cdot 31,42 cm\approx 10,05 cm$
Daraus können wir eine allgemein gültige Formel ableiten:
Merke
Merke
Formeln
Umfang:
$U = \pi \cdot d$
Kreisbogen:
$k = \frac{\alpha}{360^\circ} \cdot \pi \cdot d $
Mit den Übungsaufgaben kannst du das Berechnen von Kreisbogen und die Benennung von Geraden am Kreis einüben. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
