Was ist die Kreiszahl Pi? - Erklärung und Herleitung
Merke
$\pi = 3,14(1592654.....)$
Die Kreiszahl Pi hat das Symbol $\pi$. Sie ist eine mathematische Konstante, die das Verhältnis zwischen dem Umfang eines Kreises zu seinem Durchmesser beschreibt. Wir benötigen diese Zahl in allen möglichen Formeln rund um kreisförmige Berechnungen, aber auch in anderen Bereichen der Mathematik und Physik.
Eine Besonderheit von $\pi$ ist, dass sie irrational ist. Sie lässt sich nicht durch einen Bruch zweier ganzer Zahlen darstellen. Des Weiteren hat $\pi$ unendlich viele Nachkommastellen und besitzt keine Einheit.
Methode
Formeln mit $\pi$
Flächeninhalt Kreis:
$A = \pi \cdot r^2$
Umfang Kreis:
$U = 2 \cdot \pi \cdot r$
Geschichtliches
Die Menschheit ist schon seit langer Zeit an den Berechnungen rund um den Kreis interessiert. So benötigte man auch früher schon das Verhältnis zwischen dem Durchmesser eines Rades und seinem Umfang. Da $\pi$ genau diesem Verhältnis, zwischen Umfang und Durchmesser entspricht, wurde die Zahl im Laufe der Zeit immer genauer bestimmt.
Bereits 250 v. Chr. gelang es Archimedes die Zahl mit einem 96-Eck abzuschätzen. Erst über 2000 Jahre später bewies Johann Heinrich Lambert, dass die Zahl irrational ist. Das bedeutet, dass die Zahl nicht durch einen Bruch zweier ganzer Zahlen dargestellt werden kann.
Heutzutage wird immer noch an den billionsten Nachkommastellen geforscht.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Herleitung
Es gibt verschiedene Arten $\pi$ herzuleiten. Diese sind jedoch alle sehr kompliziert. Daher schauen wir uns hier eine einfache Herleitung an.
Für den Beweis benötigen wir die Formel des Umfangs eines Kreises.
$U=d\cdot \pi$
Der Durchmesser des Kreises soll $1 cm$ groß sein. Diesen Kreis zeichnen wir nun auf und messen anschließend den Umfang.
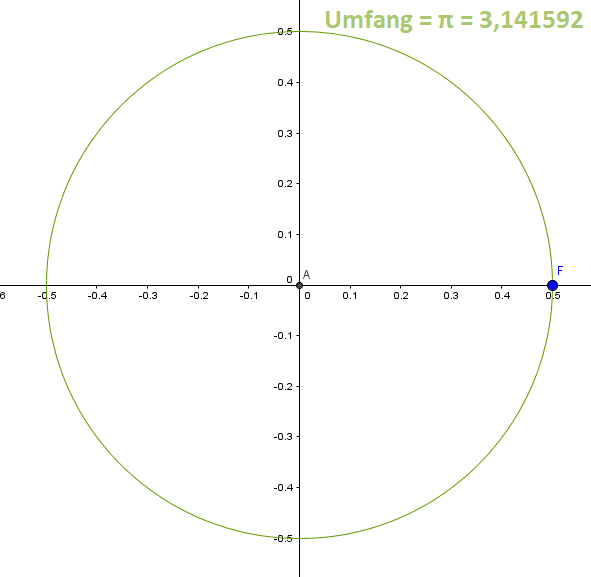
Das Programm hat gemessen, dass der Umfang des Kreises mit einem Durchmesser von $1 cm$ ungefähr $3,14 cm$ groß ist. Damit haben wir die Formel $U = \pi \cdot d$ bewiesen, aber auch gezeigt, dass $\pi$ ungefähr $3,14$ sein muss. Dabei hat $\pi$ keine Einheit.
Du kannst dies selbst einmal versuchen. Dafür musst du deinen Zirkel auf zum Beispiel $5 cm$ einstellen. Der Kreis, der dann entsteht, hat einen Durchmesser von $10 cm$. Nun kannst du einen Faden nehmen und ihn auf den Umfang legen und danach die Länge des Fadens ausmessen. Er sollte dann ungefähr $31,4 cm$ lang sein.
Gut zu wissen
Für alle beliebigen Kreise gilt: Pi ist gleich dem Umfang geteilt durch den Durchmesser. $\rightarrow \pi = \frac{U}{d}$
Wir hätten auch mit der Formel des Flächeninhalts $\pi$ abschätzen können. Denn aus $A = \pi \cdot r^2$ ergibt sich $\rightarrow \pi = \frac{A}{r^2}$.
Bogenmaß
Das Bogenmaß ist eine Art Winkelgrößen anzugeben. Die Kreiszahl $\pi$ ist ein Teil des Bogenmaßes. Meistens werden Winkel in Grad angegeben. Aber ein Winkel von $45^\circ$ kann auch im Bogenmaß, $\frac{1}{4}\pi \approx 0,79$, angegeben werden. In der Schule wird der Winkel meist in Grad angegeben, aber z.B. in der Analysis kommt das Bogenmaß vermehrt zum Einsatz.
Der Winkel wird durch die Länge des entsprechenden Kreisbogens im Einheitskreis angegeben. Die Bogenlänge ist proportional zum Radius. Daraus ergibt sich, dass ein Radius $10 cm$ mit einem Winkel von 1 rad genau $10 cm$ Bogenlänge hat.
Ein ganzer Kreis hat $360^\circ$. Die dazugehörige Bogenlänge beträgt $U = 2\cdot \pi \cdot r$. Da der Radius im Einheitskreis 1 ist, ist das Bogenmaß dann $2\cdot \pi$
Es ergeben sich folgende Umrechnungsformeln:
$1^\circ = \frac{\pi}{180^\circ}rad$
$1rad = 1\cdot \frac{180^\circ}{\pi}\approx 57,3^\circ$
Nun hast du eine detaillierte Übersicht über die Rechnungsmöglichkeiten mit Pi erhalten. Ob du alles verstanden hast, kannst du anhand unserer Übungen testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
