Schnittwinkel zweier linearer Funktionen berechnen
Lineare Funktionen, die sich schneiden, bilden einen sogenannten Schnittwinkel. Wo genau sich dieser Winkel befindet und wie man ihn berechnet, erfährst du in diesem Text.
Schnittwinkel entstehen, wenn sich lineare Funktionen schneiden. Besitzen zwei lineare Funktionen dieselbe Steigung, können sie sich nicht schneiden und dementsprechend gibt es auch keinen Schnittwinkel. Voraussetzung, um einen Schnittwinkel berechnen zu können, ist also, dass die linearen Funktionen unterschiedliche Steigungen haben.
$f(x) = \textcolor{red}{3} \cdot x -5$
$g(x) = \textcolor{red}{3} \cdot x + 7$
$\rightarrow \textcolor{red}{KEIN~SCHNITTWINKEL}$
$f(x) = \textcolor{green}{3} \cdot x -5$
$g(x) = \textcolor{green}{5} \cdot x + 7$
$\rightarrow \textcolor{green}{SCHNITTWINKEL}$
Was ist der Schnittwinkel?
Schneiden sich zwei lineare Funktionen, ergeben sich insgesamt vier verschiedene Winkel. Die gegenüberliegenden Winkel sind jeweils gleich groß, weshalb wir nur zwei unterschiedliche Bezeichnungen benötigen: $\alpha$ und $\beta$.
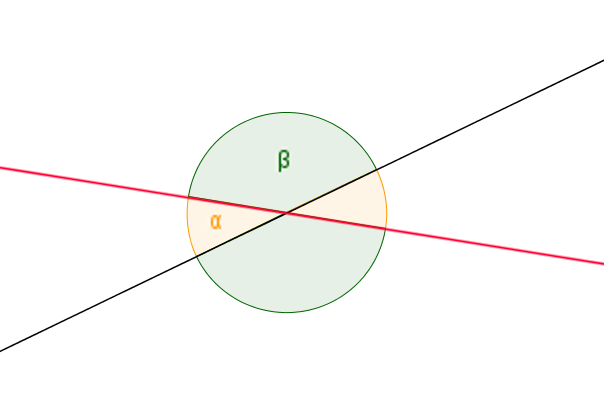
In den meisten Fällen bezeichnet man den kleineren Winkel $\alpha$ als den Schnittwinkel. Der Winkel $\beta$ wird Nebenschnittwinkel genannt.
Wie du in der Abbildung erkennen kannst, besteht eine mathematische Beziehung zwischen $\alpha$ und $\beta$.
$\alpha + \beta = 180°$
Ist der Winkel $\beta$ gegeben, kannst du den Schnittwinkel ganz einfach berechnen:
$\alpha = 180° - \beta$
Hast du die Größe des Winkels $ \beta$ nicht gegeben, musst du den Schnittwinkel mithilfe der Funktionsgleichungen berechnen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Schnittwinkel mithilfe der Funktionsgleichung berechnen
Um den Schnittwinkel aus zwei gegebenen Funktionsgleichungen zu bestimmen, musst du folgende Formel anwenden:
Merke
Berechnung des Schnittwinkels
$\large{tan~\alpha = |\frac{m_1 - m_2}{1 + m_1 \cdot m_2}|}$
Dabei entspricht $m_1$ der Steigung der einen Funktion, $m_2$ der Steigung der anderen Funktion und $tan$ dem Tangens.
Die Striche um den Bruch sind die sogenannten Betragsstriche. Den Betrag einer Zahl erhältst du, indem du das Vorzeichen weglässt:
$|+3| = 3$
$|-3| = 3$
Durch das Einsetzen der beiden Steigungen erhalten wir $tan~\alpha$. Da wir aber den Schnittwinkel $ \alpha$ und nicht den Tangens von $ \alpha$ berechnen möchten, müssen wir die Formel noch ein wenig umstellen:
$\large{tan~\alpha = |\frac{m_1 - m_2}{1 + m_1 \cdot m_2}|}$
$\large{\alpha = arctan~(|\frac{m_1 - m_2}{1 + m_1 \cdot m_2}|)}$
$arctan$ bedeutet Arcustangens und steht für die Umkehrfunktion des Tangens. Diese kannst du ganz einfach mithilfe deines Taschenrechners ausrechnen. Benutze dazu die Taste $tan^{-1}$.
Beispielaufgabe: Berechnung des Schnittwinkels
Gegeben sind diese beiden Funktionen:
$f(x) = 0,25 \cdot x + 5 \rightarrow m_1 = 0,25$
$g(x) = 2 \cdot x - 8 \rightarrow m_2 = 2$
Nun setzen wir die Steigungen in die Formel zur Berechnung des Schnittwickels ein:
$\large{tan~\alpha = |\frac{m_1 - m_2}{1 + m_1 \cdot m_2}| \Leftrightarrow tan~\alpha = |\frac{0,25 - 2}{1 + 0,25 \cdot 2}|} \Leftrightarrow tan~\alpha = |-1,167|$
$tan~\alpha = 1,167$
$\alpha = arctan (1,167)$
$\alpha \approx 49,4°$
Teste dein neu erlerntes Wissen in unseren Übungsaufgaben! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
