Kreis - So berechnest du Flächeninhalt und Umfang!
Der Kreis und seine Fläche?
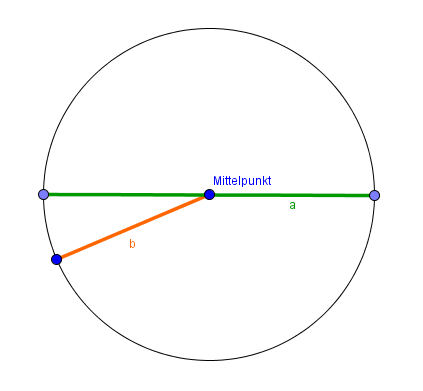
Was ist eigentlich ein Kreis? Per Definition ist es eine geometrische Figur, bei der alle Punkte den gleichen Abstand zum Mittelpunkt haben.
Ihr wisst sicher alle, wie ein Kreis aussieht. Anhand der nachfolgenden Abbildungen schauen wir uns den Kreis nochmal genauer an.
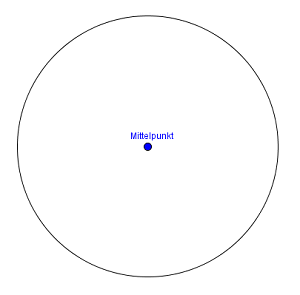
Der Mittelpunkt ist, wie der Name schon sagt, genau in der Mitte des Kreises. Der Abstand zwischen einem Punkt des Kreisrandes und dem Mittelpunkt wird als Radius bezeichnet.
Radius eines Kreises
Wenn du mit dem Zirkel einen Kreis zeichnest, stellst du als erstes einen bestimmten Radius ein. Die Spitze des Zirkels ergibt den Mittelpunkt während du mit der anderen Seite den Kreisrand bzw. die Kreislinie zeichnest. Die Größe dazwischen ist der Radius.
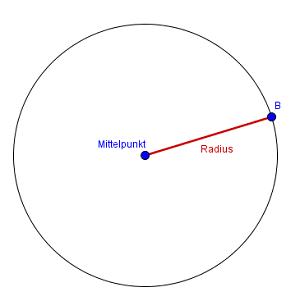
Der Radius wird vom Mittelpunkt zum Rand gemessen. Der Abstand zwischen dem Mittelpunkt und Kreisrand ist also überall gleich groß, wie es auch schon in der Definition des Kreises beschrieben wurde.
Merke
Der Radius ist Strecke zwischen dem Mittelpunkt und dem Kreisrand eines Kreises.
Kreisberechnung: Durchmesser berechnen
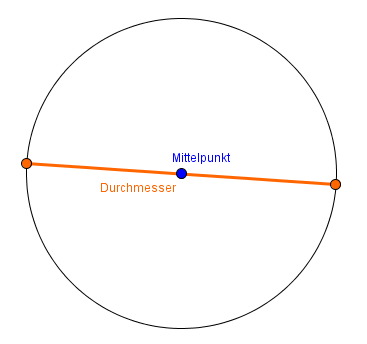
Der Durchmesser läuft von einem Punkt auf dem Rand zu dem Punkt auf der gegenüberliegenden Seite. Dabei ist es wichtig, dass die Gerade durch den Mittelpunkt läuft.
Wie dir wahrscheinlich auffällt, ist der Durchmesser doppelt so groß wie der Radius. Es gilt also:
$d=2\cdot r$ oder auch $r=0,5\cdot d$
Mit diesen Kreisformeln kannst du jeweils den Durchmesser berechnen, indem du ihn in den Radius umrechnest oder umgekehrt.
Merke
Der Durchmesser ist die Strecke zwischen zwei Randpunkten, die durch den Mittelpunkt geht.
Für das Verhältnis zwischen Durchmesser und Radius gilt folgender Zusammenhang: $d=2\cdot r$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Umfang und Kreisfläche berechnen
Fläche Kreis
Die Fläche oder der Flächeninhalt von zweidimensionalen Figuren wird in $m^2$ (Quadratmetern) angegeben. Im Gegensatz zu den rechteckigen Figuren, wie zum Beispiel dem Parallelogramm, können wir den Flächeninhalt des Kreises, also die Kreisfläche, nicht einfach berechnen, indem wir die Breite mit der Höhe multiplizieren. Der Kreis hat keine Ecken oder Kanten, auf die sich diese Formel anwenden lassen könnte. Stattdessen müssen wir auf die Eigenschaften zurückgreifen, die uns der Kreis bietet: den Radius. Eine Kreisfläche berechnet sich wie folgt:
Merke
Kreisfläche berechnen
$A=\pi \cdot r^2$
$A=\frac{\pi \cdot d^2}{4}$
Dabei ist:
A = Flächeninhalt
$\pi =$ Kreiszahl $\approx 3,14$
$r$ = Radius
$d$ = Durchmesser
Beispiel
Ein Kreis hat einen Durchmesser von $10 dm$. Wie groß ist seine Fläche? $A\approx78,54dm^2$
Wenn der Kreis einen Durchmesser von $10 dm$ hat, dann beträgt der Radius $5 dm$. Setzen wir dies in die obere Kreisflächen-Formel ein.
$A=\pi \cdot r^2$
$A=\pi \cdot 5dm^2$
$A=\pi \cdot 25dm^2\approx 78,54dm^2$
Natürlich hätten wir auch direkt mit dem Durchmesser rechnen können.
$A=\frac{\pi \cdot d^2}{4}$
$A=\frac{\pi \cdot 10dm^2}{4}$
Umfang Kreis
Der Umfang ist der Weg, den man zurücklegen muss, um einmal um einen geometrischen Körper herumzugehen. Er hat die Einheit m (Meter) und errechnet sich für den Kreis mithilfe des Radius und der Kreiszahl $\pi$.
Merke
Kreisumfang berechnen
$U=\pi \cdot d$
$U=2\cdot \pi \cdot r$
Dabei ist:
U = Umfang
$\pi =$ Kreiszahl $\approx 3,14$
$r$ = Radius
$d$ = Durchmesser
Beispiel
Ein Kreis hat einen Durchmesser von $10 dm$. Wie groß ist sein Umfang?
Setzen wir den Wert einfach in die obere Formel für den Umfang vom Kreis ein.
$U=\pi \cdot d$
$U=\pi \cdot 10dm$
$U=\pi \cdot 10dm\approx 31,42dm$
Nun hast du viel über die Berechnung der Fläche eines Kreises erfahren. Teste dein neu erlerntes Wissen zu den Themen Kreisfläche berechnen, Durchmesser berechnen und den Umfang eines Kreises berechnen online mit unseren Übungsaufgaben!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
