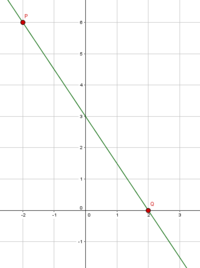
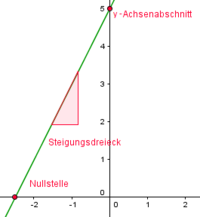
So zeichnest du eine lineare Funktion!
In diesem Kapitel befassen wir uns mit dem Zeichnen einer linearen Funktion. Dabei geben wir dir eine Schritt-für-Schritt Erklärung, wie du mithilfe einer Funktion eine Wertetabelle erstellst, wie das Koordinatensystem aussehen muss und wie die Funktion dann mithilfe der Punkte aus der Wertetabelle in dieses Koordinatensystem eingezeichnet wird.
Lineare Funktionen zeichnen
Der Begriff lineare Funktion leitet sich aus dem lateinischen ab und bedeutet so viel wie Linie. Daher muss der Funktionsgraph einer linearen Funktion auch eine Linie bzw. in der Mathematik auch Gerade genannt, sein.
Damit du den Graph einer linearen Funktion zeichnen kannst, benötigst du die Funktionsgleichung oder mindestens zwei Punkte der Funktion, um diese in ein Koordinatensystem einzuzeichnen. Diese können dann zu einer Geraden verbunden werden. Die Vorgehensweise zum Einzeichnen folgt dabei immer den gleichen Schritten:
Vorgehensweise
Merke
1. Eine Wertetabelle erstellen. Dafür müssen mehrere x-Werte in die Funktion eingesetzt werden und die dazugehörigen y-Werte ausgerechnet werden.
2. Ein passendes Koordinatensystem anlegen. Dabei musst du darauf achten, wie groß deine gegebenen Werte sind.
3. Die Punkte aus der Wertetabelle in das Koordinatensystem einzeichnen.
4. Eine Gerade durch die Punkte ziehen und die Abbildung ist fertig!
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiel: Zeichnen einer linearen Funktion
Methode
In der Wertetabelle stehen die x-Werte links und die dazugehörigen y-Werte rechts.
Ein Punkt wird mit einem Großbuchstaben bezeichnet. Dabei ist der erste Wert der x-Wert und der zweite der y-Wert:
$P ( x-Wert / y-Wert )$
In einem Koordinatensystem verläuft die $x-Achse$ immer von links nach rechts und die $y-Achse$ von unten nach oben.
Wir haben die Funktion $f(x) = 0,5 \cdot x -2$ gegeben und sollen diese in ein Koordinatensystem einzeichnen. $f(x)$ bedeutet immer das Gleiche wie $y$.
Wir gehen genauso wie bei jeder anderen Funktion vor und erstellen als erstes eine Wertetabelle. Dafür nehmen wir beliebige x-Werte und rechnen die dazugehörigen y-Werte aus.
Setzen wir für $x$ zwei beliebige Werte ein, zum Beispiel $1$ und $2$.
$y = f(1) = 0,5 \cdot 1 -2 = -1,5 \rightarrow P(1/-1,5)$
$y = f(2) = 0,5 \cdot 2 -2 = -1 \rightarrow Q(2/-1)$
Diese und weitere Punkte können wir nun in die Wertetabelle eintragen:
| x-Werte | y-Werte |
| -2 | -3 |
| -1 | -2,5 |
| 0 | -2 |
| 2 | -1 |
| 5 | 0,5 |
Dies ist eine Wertetabelle der Funktion $f(x) = 0,5 \cdot x -2 $ mit fünf verschiedenen Punkten. Einfachheitshalber verwendet man meistens die fünf x-Werte $-2$ bis $+2$.
Theoretisch reichen zwei Punkte aus, um eine lineare Funktion zu zeichnen. Alle anderen Punkte müssen auch auf der Gerade liegen. Wir nehmen zwei Punkte, die relativ weit auseinander liegen, und zeichnen diese in das Koordinatensystem ein.:
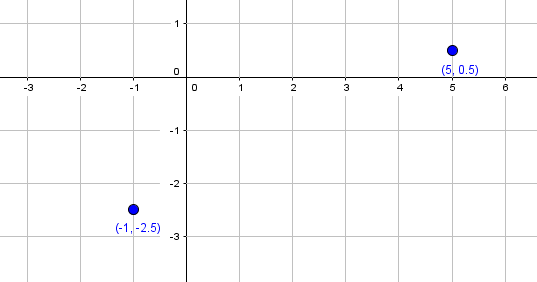
Wir haben zwei Punkte in das Koordinatensystem eingezeichnet und nun können wir durch diese Punkte eine Gerade legen. Damit erhalten wir den Graphen der Funktion.
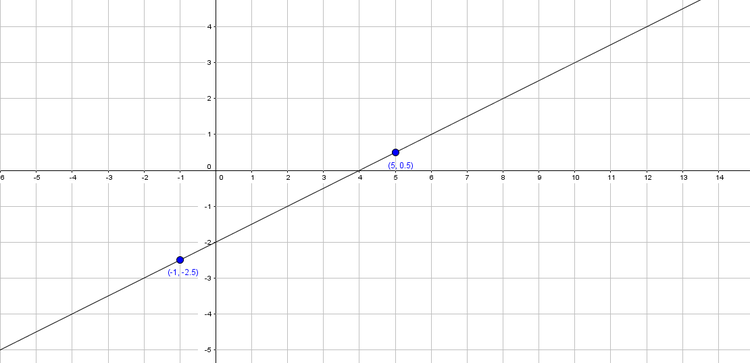
Die anderen Punkte aus der Wertetabelle müssen auch auf der Geraden liegen. In der folgenden Abbildung haben wir weitere Punkte eingetragen und stellen fest, dass diese auf der Geraden liegen:
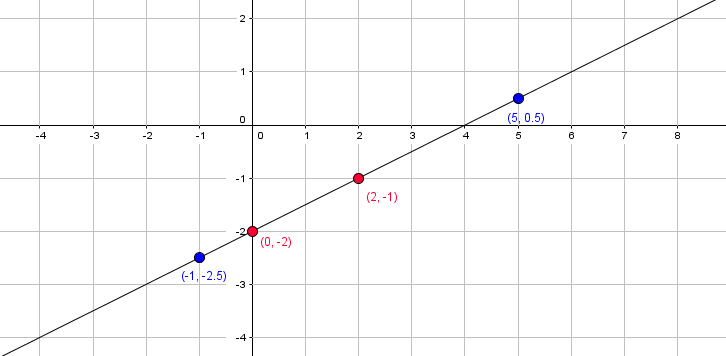
Die Gerade, die wir eingezeichnet haben, ist also die Abbildung der Funktion $f(x) = 0,5 \cdot x -2 $. Jetzt weißt du, wie du die Abbildung einer Funktion zeichnest.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Der Begriff lineare Funktion leitet sich aus dem lateinischen ab und bedeutet so viel wie ...
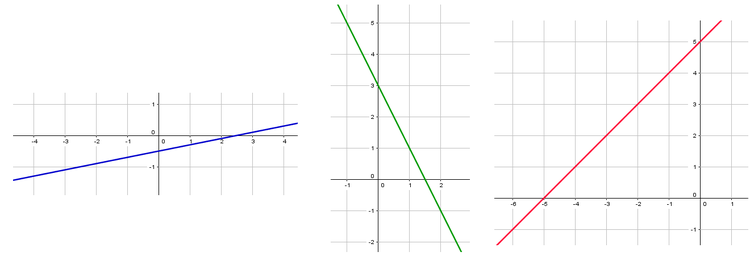
Zeichne die Funktion f(x) und vergleiche anschließend mit den Abbildungen.
Welche Funktion entspricht deiner gezeichneten Funktion?
$f(x) = -2 \cdot x +4$
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
