Nullstelle einer linearen Funktion bestimmen
In der Analysis ist das Bestimmen der Nullstellen von elementarer Bedeutung. Eine lineare Funktion kann nur eine oder keine Nullstelle haben. Wie man die Nullstelle einer Funktion ablesen bzw. berechnen kann, klären wir in diesem Kapitel.
Nullstelle einer linearen Funktion graphisch bestimmen
Eine Nullstelle ist ein Schnittpunkt mit der $x-Achse$. Also gehen wir ähnlich vor, wie beim Bestimmen des y-Achsenabschnitts.
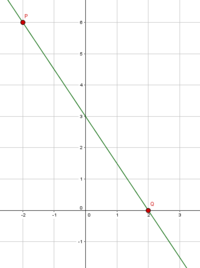
Wenn die Abbildung eines Graphen gegeben ist, können wir die Nullstelle einfach bei der Funktion ablesen, solange der Punkt genau erkennbar ist:
Die Nullstelle liegt am Punkt $N(1/0)$. Bei einer Nullstelle ist der $y-Wert$ immer null. $\rightarrow N(x/\textcolor{BrickRed}{0})$. Du hast also gerade gelernt, wie du bei der Funktion die Nullstelle ablesen, also graphisch bestimmen kannst. Natürlich ist dies nicht immer möglich, weswegen es noch ein anderes Verfahren gibt: Du kannst rechnerisch Nullstellen bestimmen.
Nullstelle rechnerisch bestimmen
Die Nullstelle befindet sich dort, wo der $y-Wert$ null ist. Also muss, um den Nullpunkt zu berechnen, die lineare Funktion gleich null gesetzt werden. Schauen wir uns dies rechnerisch an einem Beispiel an:
Beispiel
Beispiel
Bestimme die Nullstelle der Funktion $f(x) = y = 3\cdot x +6$
1. Die Funktion gleich null setzen
$f(x) = 3\cdot x +6 \textcolor {BrickRed}{= 0}$
2. nach x auflösen
$0 = 3\cdot x +6$ $|-6$
$-6 = 3\cdot x$ $|:3$
$\frac{-6}{3} = -2 = x$
3. Nullstelle aufschreiben
Die Nullstelle hat den $x-Wert: - 2$.
$N(-2/0)$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Vorgehensweise: Nullstelle berechnen
Methode
Methode
- Die Funktion gleich null setzen.
- Nach $x$ auflösen.
- Nullstelle aufschreiben.
Beispielaufgaben: Nullstelle von linearen Funktionen bestimmen
Bestimme je die Nullstelle der Funktionen!
a) $f(x) = -0,5 \cdot x + 2 $
b) $g(x) = 50 \cdot x +25$
c) $h(x) = -x-1,75$
a) $f(x) = -0,5 \cdot x + 2 $
1. Die Funktion gleich null setzen
$f(x) = -0,5 \cdot x +2 = 0$
2. nach $x$ auflösen
$0 = -0,5 \cdot x + 2$ $|-2$
$-2 = -0,5 \cdot x$ $|:(-0,5)$
$\frac{-2}{-0,5} = 4 = x$
3. Nullstelle aufschreiben
$N_f(4/0)$
b) $g(x) = 50 \cdot x +25$
$g(x) = 50 \cdot x +25 = 0$ $|-25$
$-25 = 50 \cdot x$ $|:50$
$\frac{-25}{50} = -0,5 = x$
$N_g(-0,5/0)$
c) $h(x) = -x-1,75$
$h(x) = - x - 1,75 = 0$ $|+1,75$
$1,75 = -x$ $|:(-1)$
$-1,75 = x$
$N_h(-1,75/0)$
Lineare Funktionen ohne Nullstelle
Jede lineare Funktion hat entweder eine Nullstelle oder keine Nullstelle. Funktionen, die keine Nullstelle besitzen, verlaufen parallel zur $x-Achse$.
Diese Gerade wird die $x-Achse$ nie schneiden.
$f(x) = y= m\cdot x +n \rightarrow$ Die Steigung einer Funktion, die keine Nullstelle besitzt, ist null. $m = 0$
$f(x) = y = 0 \cdot x +3 = 3$
$f(x) = y = 3$
Eine lineare Funktion, die eine Parallele zur $x-Achse$ ist, hat keinen Wert für $x$ bzw. er ist null. Somit gibt es keinen Schnittpunkt mit der x-Achse.
Gut zu wissen
Hinweis
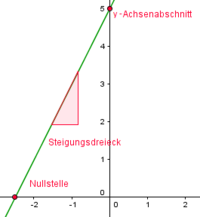
An einer linearen Funktion kannst du ebenso die Steigung bestimmen, oder auch den y-Achsenabschnitt. In den Lerntexten Steigung einer linearen Funktion bestimmen - Steigungsdreieck und y-Achsenabschnitt einer linearen Funktion bestimmen und berechnen kannst du jetzt mehr dazu erfahren.
Jetzt weißt du alles Wichtige über das Bestimmen der Nullstelle einer linearen Funktion. Du kannst dich noch weiter mit Hilfe der Übungsaufgaben testen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang