Umkehrfunktion einer linearen Funktion berechnen
In diesem Lerntext erklären wir dir die Vorgehensweise zur Berechnung der Umkehrfunktion einer linearen Funktion. Diese Vorgehensweise zeigen wir dir anhand mehrerer Beispiele.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Umkehrfunktion einer linearen Funktion berechnen
Die Umkehrfunktion einer linearen Funktion lässt sich mithilfe weniger Schritte aufstellen. Nachfolgend siehst du die Vorgehensweise beim Berechnen der Umkehrfunktion einer linearen Funktion:
Methode
1. Funktion nach $x$ auflösen.
2. $x$ und $f(x)$ vertauschen.
Wenden wir diese beiden Schritte einmal auf ein Beispiel an:
1. Funktion nach $x$ auflösen
$f(x) = 2 \cdot x +1~~~~~~|-1$
$f(x) - 1 = 2 \cdot x~~~~~| :2$
$\frac{f(x)}{2} - 0,5 = x$
2. $x$ und $f(x)$ vertauschen
$0,5 \cdot f(x) - 0,5 = x~~~~~|f(x) \leftrightarrow x$
$f(x) = 0,5 \cdot x - 0,5$
Gut zu wissen
Um deutlich zu machen, dass es sich um eine Umkehrfunktion handelt, schreibt man anstatt $f(x)$ auch $f^{-1}(x)$.
$\rightarrow f^{-1}(x) = 0,5 \cdot x - 0,5$
Schauen wir uns einige weitere Beispiele an, um das Vorgehen besser zu verstehen.
Beispiel
$f(x) = 5 \cdot x +10$
$f(x) = 5\cdot x + 10~~~~~|-10$
$f(x) - 10 = 5 \cdot x~~~~~|:5$
$\frac{f(x)}{5} - 2 = x$
$\frac{1}{5} \cdot f(x) - 2 = x~~~~~|f(x) \leftrightarrow x$
$\frac{1}{5} \cdot x - 2 = f(x)$
$\rightarrow f^{-1}(x) = \frac{1}{5} \cdot x - 2$
Beispiel
$f(x) = 12 \cdot x +30$
$f(x) = 12 \cdot x + 30~~~~~|-30$
$f(x) - 30 = 12 \cdot x~~~~~|:12$
$\frac{f(x)}{12} - 2,5 = x$
$\frac{1}{12} \cdot f(x) - 2,5 = x~~~~~|f(x) \leftrightarrow x$
$\frac{1}{12} \cdot x - 2,5 = f(x)$
$\rightarrow f^{-1}(x) = \frac{1}{12} \cdot x - 2,5$
Beispiel
$f(x) = x - 15$
$f(x) = x - 15~~~~~|+15$
$f(x) + 15 = x~~~~~|f(x) \leftrightarrow x$
$x +15 = f(x)$
$\rightarrow f^{-1}(x) = x + 15$
Grafische Bedeutung der Umkehrfunktion
Das grafische Eintragen der Umkehrfunktion funktioniert genauso, wie bei der normalen Funktion. In der Abbildung siehst du die Ausgangsfunktion $\textcolor{green}{f(x) = 2 \cdot x +1}$ in Grün und ihre entsprechende Umkehrfunktion $\textcolor{red}{f^{-1}(x) = 0,5 \cdot x - 0,5}$ in Rot. Zusätzlich zu diesen beiden Funktionen ist auch noch die Winkelhalbierende ($f(x) = x$) eingezeichnet.
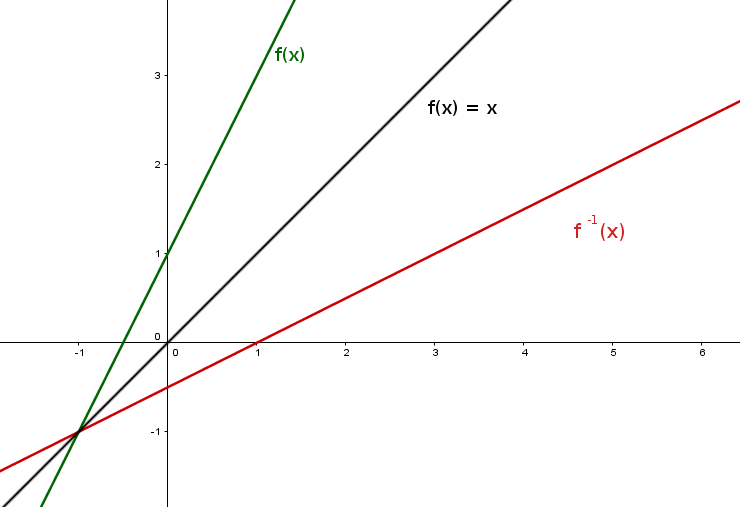
Zwischen der Funktion und der Umkehrfunktion besteht ein grafischer Zusammenhang: Spiegelt man alle Punkte der Ausgangsfunktion $f(x)$ an der Winkelhalbierenden, erhält man die Umkehrfunktion $f^{-1}(x)$.
Teste dein neues Wissen zum Berechnen von Umkehrfunktionen mit unseren Aufgaben! Viel Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
