Satz des Pythagoras - Textaufgabe mit Lösungen
Der Satz des Pythagoras ist nicht nur in Dreiecken hilfreich. Wir werden jetzt sehen, dass wir die eben gelernte Formel auch bei Vierecken anwenden können.
Beispielaufgabe
Schauen wir uns gemeinsam folgendes Problem an. Wir haben ein Viereck mit einer unbekannten Seitenlänge $b$.
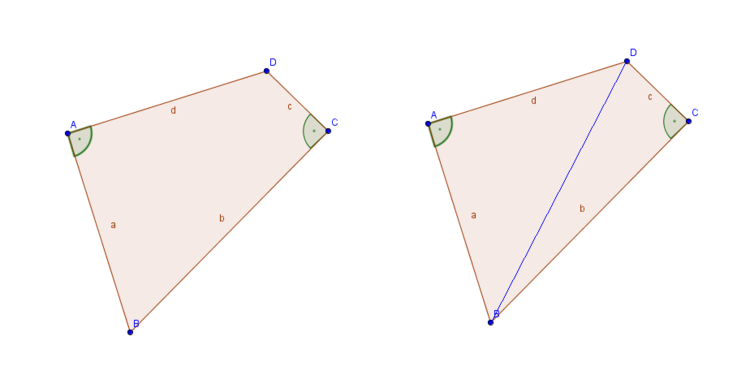
Wie du in der Abbildung erkennen kannst, lässt sich das gegebene Viereck in zwei rechtwinklige Dreiecke zerschneiden. Wie schon bei den Dreiecks-Aufgaben fehlt eine Seitenlänge des Vierecks. Die Seiten $a$, $c$ und $d$ sind gegeben. Um also $b$ zu berechnen reicht uns eigentlich das rechte Dreieck $BCD$. Allerdings fehlen uns in diesem Dreieck zwei Seitenlängen, nämlich die unbekannte Länge $b$ und die Länge der gezogen Trennlinie ($h$). Der Satz des Pythagoras bringt uns an dieser Stelle nicht weiter. Unsere einzige Möglichkeit ist zunächst das linke Dreieck zu betrachten. Auch hier ist die Länge der Trennlinie unbekannt. Im Gegensatz zur rechten Hälfte sind uns aber die beiden anderen Seitenlängen bekannt, sodass wir die Länge der Trennlinie ($h$) berechnen können.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Lösungsweg
Berechnen wir also zunächst die Länge von $h$ im Dreieck $ABD$. Dieses Beispiel ist besonders einfach, da die gesuchte Länge die Hypotenuse ist, also dem rechten Winkel gegenüber liegt. Wir müssen den Satz des Pythagoras also gar nicht umstellen, sondern rechnen direkt mit den Quadraten der Katheten $a$ und $d$.
$a^2 + d^2 = h^2$
$(12 cm)^2 + (9 cm)^2 = h^2$
$225 cm^2 = h^2$ | $\sqrt[]{}$
$\sqrt[]{225cm^2} = h$
$h = 15 cm$
Wir kennen jetzt die Länge der Trennlinie $h$ und haben im rechten Dreieck $BCD$ nur noch eine unbekannte Seite. In diesem Fall ist die unbekannte Seitenlänge $b$ jedoch eine der Katheten, sodass wir den Satz des Pythagoras zunächst umformen müssen:
$b^2 + c^2 = h^2$ | $-c^2$
$b^2 = h^2 - c^2$ |$\sqrt[]{}$
$b = \sqrt[]{(15 cm)^2 - (5 cm)^2}$
$b \approx 14,14 cm$
Der Satz des Pythagoras kann also auch bei Vielecken (mehreckigen Figuren) angewendet werden. Das Prinzip ist dabei immer dasselbe: Wir zerlegen die Figur in möglichst wenige, rechtwinklige Dreiecke und rechnen dann nacheinander alle unbekannten Größen aus.
Merke
Der Satz des Pythagoras kann also auch bei Vielecken (mehreckigen Figuren) angewendet werden. Das Prinzip ist dabei immer dasselbe: Wir zerlegen die Figur in möglichst wenige, rechtwinklige Dreiecke und rechnen dann nacheinander alle unbekannten Größen aus.
In den Übungsaufgaben kannst du jetzt dein neues Wissen testen. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Wie viele rechtwinklige Dreiecke findest du in diesem Trapez?
(Gefundene Dreiecke dürfen nicht in noch weitere Dreiecke zerlegt werden.)
Wie viele Größen dürfen unbekannt sein, um den Satz des Pythagoras anwenden zu können?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
