Quader und Würfel: Formeln für Fläche und Volumen
Der Quader ist eine dreidimensionale Darstellung eines Rechtecks. Er besteht aus $8$ Ecken und $12$ Kanten und wird von $6$ Rechtecken gebildet. Die gegenüberliegenden Rechtecke sind deckungsgleich, das heißt sie passen genau aufeinander. Man nennt diese Eigenschaft auch Kongruenz. An jeder Ecke laufen drei Kanten zusammen.
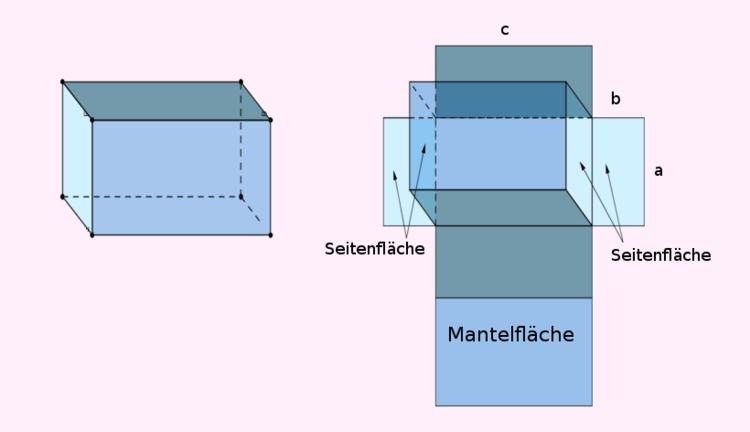
Oberfläche eines Quaders
Die vier großen Rechtecke bilden die Mantelfläche des Quaders, die zwei kleineren Rechtecke sind die Seitenflächen. Seiten- und Mantelfläche bilden zusammen die Oberfläche. Um die einzelnen Flächen zu berechnen, musst du die Länge mit der Breite multiplizieren.
$ O = 2\cdot Seitenfläche~+~Mantelfläche~= 2 \cdot (a\cdot b) + (2\cdot a \cdot c + 2\cdot b\cdot c) = 2\cdot (a \cdot b + a\cdot c + b\cdot c)$
Merke
Merke
Oberfläche eines Quaders mit den Seitenlängen $a$, $b$, und $c$.
$O= 2\cdot (a \cdot b + a\cdot c + b\cdot c)$
Beispiel
Beispiel
Wie groß ist die Oberfläche eines Quaders mit folgenden Seitenlängen?
$a = 5~cm$, $b = 2~cm$, $c= 8~cm$
$O= 2\cdot (5~cm \cdot 2 ~cm + 5~cm \cdot 8~cm + 2~cm \cdot 8~cm) = 132~cm^2$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Volumen eines Quaders
Um das Volumen eines Quaders auszurechnen, musst du die Länge, Breite und Höhe miteinander multiplizieren.
Merke
Merke
Volumen eines Quaders
$V=~Länge~\cdot ~Breite ~\cdot ~ Höhe$
$V = a \cdot b \cdot c$
Beispiel
Beispiel
Welches Volumen hat ein Quader mit den folgenden Seitenlängen?
$a = 4~cm$, $b = 2~cm$, $c= 7~cm$
$V = 4~cm \cdot 2~cm \cdot 7~cm = 56~cm^3$
Der Würfel - Ein Sonderfall des Quaders
Bei dem Würfel handelt es sich um einen Sonderfall des Quaders. Auch der Würfel besitzt $8$ Ecken und $12$ Kanten. Außerdem wird er von $6$ deckungsgleichen Quadraten gebildet. Die Kanten des Würfels sind alle gleich lang.
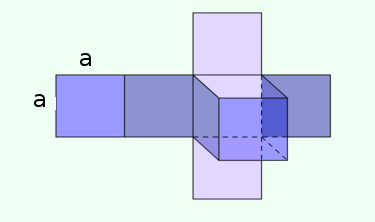
Oberfläche eines Würfels
Die Oberfläche eines Würfels besteht aus den sechs deckungsgleichen Quadraten, deren Flächeninhalte einfach addiert werden müssen.
Merke
Merke
$O_{Würfel}= 6 \cdot a \cdot a = 6\cdot a^2$
Beispiel
Beispiel
Wie groß ist die Oberfläche eines Würfels mit der Kantenlänge $7~cm$?
$O= 6 \cdot a^2 = 6\cdot (7~cm)^2 = 6 \cdot 49~cm^2 = 294~cm^2$
Volumen eines Würfels
Das Volumen eines Würfels berechnest du wie beim Quader, indem du die Länge, Breite und Höhe miteinander multiplizierst. Da die jeweiligen Kanten alle gleich groß sind, erhalten wir einen simplen Ausdruck.
Merke
Merke
$V_{Würfel} = a \cdot a \cdot a = a^3$
Beispiel
Beispiel
Wie groß ist das Volumen eines Würfels mit der Kantenlänge $5~cm$?
$V = a^3 = (5~cm)^3 = 125~cm^3$
Jetzt hast du einen detaillierten Überblick über die Oberflächen- und Volumenberechnung von Würfeln und Quadern erhalten. Ob du alles verstanden hast, kannst du nun anhand unserer Übungen testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
