Was ist ein Prisma? - Volumen und Oberfläche berechnen
Habt ihr gerade in Mathe in Geometrie das Prisma als Thema? Lernt ihr gerade alles zum Thema Prisma? Hier lernst du alles Wichtige über den geometrischen Körper, das Prisma. Wir erklären dir, wie du zum Beispiel das Volumen berechnest, wie du bei der Oberflächenberechnung vorgehst und wenden dies direkt in Aufgaben mit echten Prismen an.
Prisma - Formeln und Fakten
Wir haben dir hier schon mal das Wichtigste zum geometrischen Körper, dem Prisma aufgelistet:
Methode
Methode
- Die Grundflächen von Prismen können unterschiedlich aussehen. Die Grundfläche kann zum Beispiel ein Dreieck ("dreieckiges Prisma") oder ein Sechseck ("sechseckiges Prisma") sein.
- Das Volumen eines Prismas berechnest du, indem du die Formel $V_{Prisma} = G ~ \cdot ~h$ anwendest. Die Formel der Grundfläche $G$ variiert je nach Form der Grundfläche.
- Die Oberfläche eines Prismas berechnest du, indem du die Formel $A_{Mantel} = U_{Grundfläche} \cdot h_{Prisma}$ anwendest. Hier variieren sowohl die Flächeninhaltsformel der Grundfläche als auch die der Mantelfläche.
Im Folgenden erklären wir dir diese Informationen nun detaillierter und geben dir Beispiele an die Hand.
Prisma: Definition
Im Gegensatz zur Kugel oder zum Zylinder ist ein Prisma in der Geometrie laut Definition kein eindeutig definierter Körper. Man kann ein Prisma vielmehr als eine Gruppe oder Art von geometrischen Körpern bezeichnen, dessen Grundfläche ein beliebiges Vieleck (z. B. Dreieck, Sechseck) ist. Alle Seitenkanten sind parallel zueinander und gleich lang. Die Grundfläche und die Deckfläche sind daher identisch.
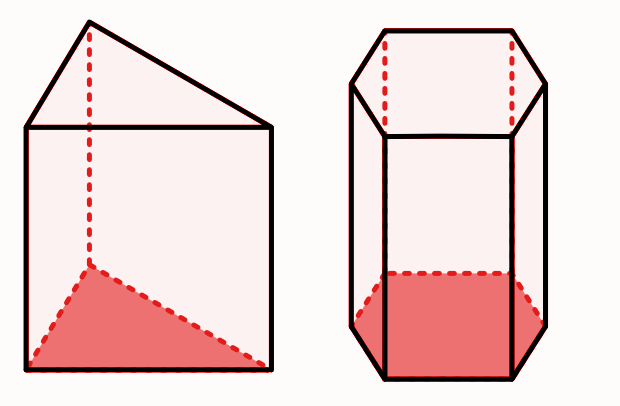
Wie bei allen geometrischen Körpern können wir also auch bei einem Prisma Grund-, Deck- und Mantelfläche unterscheiden. Die folgende Abbildung zeigt zwei beispielhafte Prismen. Die Grundfläche bzw. Deckfläche des linken Prismas ist ein Dreieck. Die Mantelfläche besteht aus drei Rechtecken. Wenn man die Mantelfläche aufklappt, ergeben diese drei Rechtecke zusammen ein großes Rechteck. Die Grundfläche bzw. Deckfläche des rechten Prismas ist ein Sechseck. Der Mantel besteht aus sechs Rechtecken. Wenn man die Mantelfläche aufklappt, ergeben diese sechs Rechtecke zusammen auch wieder ein großes Rechteck. Die Mantelfläche eines Prismas ist also immer ein Rechteck, unabhängig von der Form der Grundfläche.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Volumen berechnen: Prisma
Da ein Prisma, je nach Grundfläche, unterschiedliche Formen annehmen kann, können wir keine konkrete allgemeingültige Prisma-Formel zur Berechnung des Volumens angeben.
Dennoch können wir eine, wenn auch relativ allgemeine, Formel zur Berechnung des Volumens angeben. (Diese Prisma-Formel ähnelt den Formeln zur Berechnung des Volumens eines Quaders bzw. eines Würfels.)
Merke
Merke
$V_{Prisma} = G ~ \cdot ~h$
$G$ = Grundfläche
$h$ = Höhe des Prismas
Da die Form der Grundfläche variabel ist, können wir keine konkretere Formel aufstellen.
Beispiel
Beispiel
Berechne das Volumen des beschriebenen Prismas:
Die Grundfläche des Prismas ist ein Dreieck. Die Grundseite des Dreiecks ($g_D$) beträgt $6~cm$ und die Höhe des Dreiecks ($h_D$) beträgt $4~cm$. Die Höhe des Prismas ($h_{Prisma}$) beträgt $12~cm$.
In unserem Beispiel ist die Grundseite ein Dreieck. Wir benötigen also zunächst den Flächeninhalt des Dreiecks. Die Formel dazu lautet:
$G_{Prisma}=A_{Dreieck} = \frac{1}{2} \cdot g_D \cdot h_D$
Da wir nun wissen, wie wir die Grundfläche des Prismas berechnen müssen, können wir die Formel für das Volumen des Prismas neu aufstellen:
$V_{Prisma} = G_{Prisma} ~ \cdot ~h_{Prisma}$
$\leftrightarrow~~~V_{Prisma} = \frac{1}{2} \cdot g_D \cdot h_{D} \cdot h_{Prisma}$
Nun setzen wir die gegebenen Werte ein und erhalten:
$V_{Prisma} = \frac{1}{2} \cdot 6~cm~ \cdot 4~cm~ \cdot 12~cm~=~144~cm^3$
Oberfläche berechnen
Auch bei der Oberfläche, bzw. dem Oberflächeninhalt können wir nur eine ganz allgemeine Prisma-Formel aufstellen. So setzt sich die Oberfläche eines Prismas aus dem Flächeninhalt der Deck-, der Grund- und der Mantelfläche zusammen.
$O_{Prisma} = A_{Grundfläche} + A_{Deckfläche} + A_{Mantelfläche}$
Da Grund- und Deckfläche gleich groß sind, können wir die Formel vereinfachen:
Merke
Merke
$O_{Prisma} = 2\cdot A_{Grundfläche} + A_{Mantelfläche}$
Je nachdem welche Form die Grundfläche des Prismas besitzt, musst du die richtige Prisma-Formel für das entsprechende Vieleck finden.
Die Mantelfläche eines Prismas ist immer ein Rechteck. Die beiden Seitenlängen dieses Rechtecks sind bekannt: Die eine Seitenlänge des Rechtecks entspricht dem Umfang der Grundfläche ($U_{Grundfläche}$) und die andere Seitenlänge entspricht der Höhe des Prismas ($h_{Prisma}$). Für die Berechnung der Mantelfläche können wir also eine Formel aufstellen:
Merke
Merke
$A_{Mantel} = U_{Grundfläche} \cdot h_{Prisma}$
Beispiel
Beispiel
Berechne die Oberfläche des folgenden Prismas.
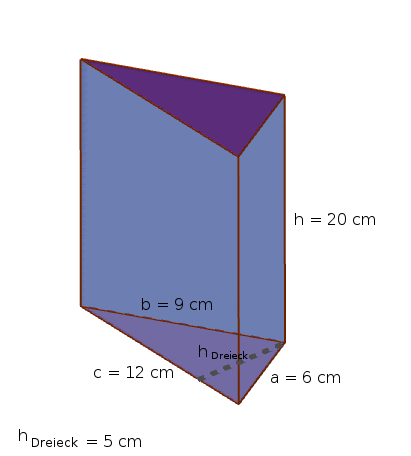
Die Grund- und Deckfläche des Prismas sind dreieckig. Der Flächeninhalt eines Dreiecks berechnet sich nach folgender Formel:
$A_{Dreieck} = \frac{1}{2} \cdot g_D \cdot h_D$
$g_D$ = Grundseite des Dreiecks
$h_D$ = Höhe des Dreiecks
Grundseite und Höhe des Dreiecks können wir aus der Zeichnung ablesen.
$A_{Grundfläche} = \frac{1}{2} \cdot 12~cm \cdot 5~cm = 30~cm^2$
Als nächstes berechnen wir die Mantelfläche:
$A_{Mantel} = U_{Grundfläche}\cdot h_{Prisma} = (9~cm + 12~cm + 6~cm) \cdot 20~cm = 540~cm^2$
Haben wir Grund- und Mantelfläche berechnet, müssen wir die Werte nur noch addieren und erhalten so die Oberfläche des Prismas:
$O_{Prisma} = 2\cdot A_{Grundfläche} + A_{Mantelfläche} = 2\cdot 30~cm^2 + 540~cm^2 = 600~cm^2$
Nun hast du alles Wichtige gelernt, was du an Prismen berechnen kannst. Teste dein neu erlerntes Wissen zu Prismen in unseren Übungsaufgaben!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Ein Prisma besitzt als Grundfläche ein rechtwinkliges Dreieck. Die Katheten des Dreiecks sind $3~cm$ und $5~cm$ lang. Die Höhe des Prismas beträgt $10~cm$. Wie groß ist die Mantelfläche?
Welche Form hat die Grundfläche eines Prismas?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
