Was sind platonische Körper?
In diesem Lerntext befassen wir uns mit den sogenannten platonischen Körpern. Sie gehören zur Gruppe der zusammengesetzten Körper und wir können ihre Oberfläche und ihr Volumen mittels bestimmter Formeln berechnen.
Was ist ein platonischer Körper?
Ein platonischer Körper ist ein Körper, der aus regelmäßigen Vielecken zusammengesetzt ist. Wichtig ist dabei, dass an jeder Ecke des Körpers gleich viele Vielecke aufeinandertreffen. Ist dies nicht der Fall, bezeichnet man den Körper auch nicht als platonisch.
Wie viele platonische Körper gibt es?
Die oben genannte Definition schränkt unsere Möglichkeiten ein, denn obwohl es beliebige viele Vielecke gibt, können wir lediglich fünf platonische Körper konstruieren. Diese platonischen Körper lauten: Tetraeder, Hexaeder (oder: Würfel), Oktaeder, Pentagondodekaeder und Ikosaeder. Wie diese Körper aussehen, sieht du in der unteren Abbildung.
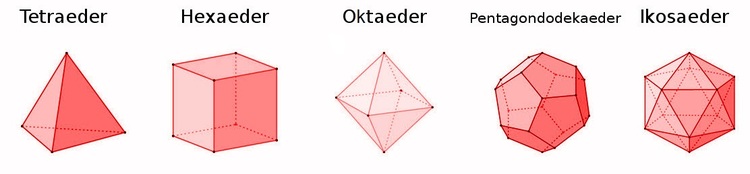
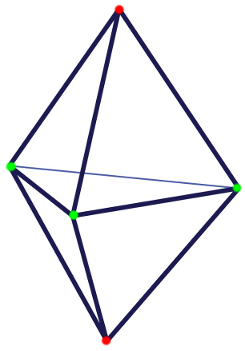
Es gibt nur diese fünf platonischen Körper, da bei allen anderen, aus Vielecken zusammengesetzten Körpern an ihren Ecken nicht gleich viele Vielecke aufeinandertreffen. Ein gutes Beispiel sind zwei zusammengesetzte Tetraeder. Dieser Körper wird zwar aus regelmäßigen Vielecken aufgebaut, allerdings treffen an seinen Ecken mal drei ($\textcolor{red}{rot}$) und mal vier ($\textcolor{green}{gruen}$) Vielecke aufeinander.
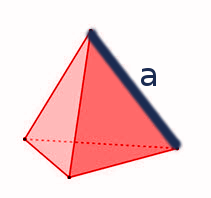
Wenn wir mit platonischen Körpern rechnen, ist für uns vor allem eine Größe wichtig: die Seitenlänge $a$. Mithilfe dieser Angabe können wir Oberfläche und Volumen der Körper berechnen. Schauen wir uns nun die einzelnen Körper genauer an. Die Herleitung der Formeln zur Berechnung von Oberfläche und Volumen sind sehr anspruchsvoll und werden an dieser Stelle vorerst nicht behandelt.
Tetraeder
Der einfachste platonische Körper ist der Tetraeder, da er aus vier gleichseitigen Dreiecken zusammengesetzt wird (tetra = vier). Sein Netz ist ebenfalls ein gleichseitiges Dreieck.
Der Tetraeder besitzt...
- 4 Eckpunkte,
- 6 Kanten und
- 4 Seitenflächen.
Merke
Der Tetraeder ist aus vier gleichseitigen Dreiecken zusammengesetzt.
Volumen eines Tetraeders
$V_{Tetraeder} = \frac{\sqrt[]{2}}{12} \cdot a^3 \approx 0,1179 \cdot a^3$
Oberfläche eines Tetraeders
$O_{Tetraeder} = \sqrt[]{3} \cdot a^2 \approx 1,7321 \cdot a^2$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Hexaeder (Würfel)
Der Hexaeder, oder auch einfach Würfel, ist der bekannteste platonische Körper. Er ist aus sechs Quadraten zusammengesetzt (hexa = sechs) und ist somit nichts anderes als ein Quader, dessen Seitenlängen alle gleich lang sind.
Der Hexaeder besitzt...
- 8 Eckpunkte,
- 12 Kanten und
- 6 Seitenflächen.
Merke
Der Hexaeder ist aus sechs Quadraten zusammengesetzt.
Volumen eines Hexaeders
$V_{Hexaeder} = a^3$
Oberfläche eines Hexaeders
$O_{Hexaeder} = 6 \cdot a^2$
Oktaeder
Der Oktaeder ist wie der Tetraeder aus gleichseitigen Dreiecken aufgebaut. Im Gegensatz zum Tetraeder sind es beim Oktaeder aber gleich acht gleichseitige Dreiecke (octa = acht). Der Oktaeder erinnert an zwei quadratische Pyramiden, die an ihren Grundflächen zusammengesetzt wurden.
Der Oktaeder besitzt...
- 6 Eckpunkte,
- 12 Kanten und
- 8 Seitenflächen.
Merke
Der Oktaeder ist aus acht gleichseitigen Dreiecken zusammengesetzt.
Volumen eines Oktaeders
$V_{Oktaeder} = \frac{\sqrt[]{2}}{3} \cdot a^3 \approx 0,4714 \cdot a^3$
Oberfläche eines Oktaeders
$O_{Oktaeder} = 2\cdot \sqrt[]{3} \cdot a^2 \approx 3,4641 \cdot a^2$
Pentagondodekaeder
Der Pentagondodekaeder, in der Kurzform auch einfach Dodekaeder, besteht aus zwölf regelmäßigen Fünfecken (dodeka = zwölf). Seine äußere Form erinnert ein wenig an eine Kugel.
Der Dodekaeder besitzt...
- 20 Eckpunkte,
- 30 Kanten und
- 12 Seitenflächen.
Merke
Der Dodekaeder ist aus zwölf regelmäßigen Fünfecken zusammengesetzt.
Volumen eines Dodekaeders
$V_{Dodekaeder} = \frac{15 + 7 \cdot \sqrt[]{5}}{4} \cdot a^3 \approx 7,6631 \cdot a^3$
Oberfläche eines Dodekaeders
$O_{Dodekaeder} = 3 \cdot \sqrt[]{25 + 10 \cdot \sqrt[]{5}} \cdot a^2 \approx 20,6457 \cdot a^2$
Ikosaeder
Der Ikosaeder besteht aus 20 gleichseitigen Dreiecken (eikosa = zwanzig) und hat ebenfalls eine rundliche Erscheinungsform.
Der Ikosaeder besteht aus...
- 12 Eckpunkte,
- 30 Kanten und
- 20 Seitenflächen.
Merke
Der Ikosaeder ist aus 20 gleichseitigen Dreiecken zusammengesetzt.
Oberfläche eines Ikosaeders
$O_{Ikosaeder} = 5 \cdot \sqrt[]{3} \cdot a^2 \approx 8,6603 \cdot a^2$
Volumen eines Ikosaeders
$V_{Ikosaeder} = \frac{5 \cdot (3 + \sqrt[]{5})}{12} \cdot a^3 \approx 2,1817 \cdot a^3$
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
