Ihr nehmt gerade die Pyramide in Geometrie in Mathe durch? In diesem Lerntext lernst du den Aufbau einer Pyramide kennen. Außerdem lernst du, wie du die Grundfläche, Mantelfläche, Oberfläche und das Volumen einer Pyramide berechnen kannst. Wir zeigen dir dazu alle wichtigen Formeln und wie diese Formeln hergeleitet werden.
Was ist eine Pyramide? - Übersicht
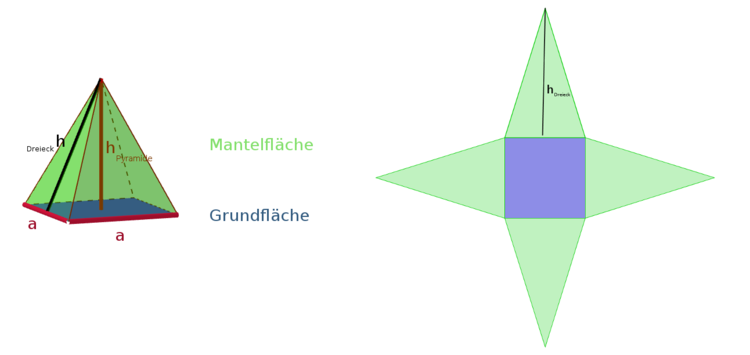
Die Pyramide ist ein geometrischer Körper, der aus einem Vieleck als Grundfläche, mindestens 3 gleichschenkligen Dreiecken als Mantelfläche und einer Spitze besteht. Die Mantelfläche einer Pyramide besitzt genauso viele Dreiecke, wie die Grundfläche Seiten hat. Die regelmäßige Form einer Pyramide besteht aus einem Quadrat als Grundfläche und entsprechend vier kongruenten gleichschenkligen Dreiecken. Wichtige Größen der Pyramide sind die Seitenlänge $a$ der Grundfläche, die Höhe $h_{Py}$ der Pyramide und die Höhe $h_{Dreieck}$ der Dreiecke. Die Höhe der Pyramide reicht vom Mittelpunkt der Grundfläche, d.h. dem Schnittpunkt der Diagonalen, bis zur Spitze.
Darüber hinaus gibt es weitere Arten von Pyramiden, die alle unterschiedliche Grundflächen besitzen. Eine Pyramide mit einem Dreieck als Grundfläche nennt man dreiseitige Pyramide, weil ihre Mantelfläche jeweils drei Seiten hat. Analog dazu nennt man Pyramiden mit einem Fünfeck als Grundfläche fünfseitige Pyramiden und solche mit einem Sechseck als Grundfläche sechsseitige Pyramiden.
Methode
- Grundfläche berechnen: $A_{Grundfläche} = a \cdot a = a^2$
- Oberfläche berechnen: $O_{Pyramide} = a^2 + 4 \cdot (\frac{1}{2} \cdot a \cdot h_{Dreieck})$
- Mantelfläche berechnen: $A_{Mantel} = 4 \cdot (\frac{1}{2} \cdot a \cdot h_{Dreieck})$
- Volumen berechnen: $V_{Pyramide} = \frac{1}{3} \cdot a^2 \cdot h_{Pyramide}$
Die Berechnungen zur Grundfläche, Oberfläche, Mantelfläche und zum Volumen an der Pyramide werden im Folgenden beispielhaft anhand einer vierseitigen Pyramide erklärt.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Pyramide berechnen: Grundfläche
Die Grundfläche einer vierseitigen Pyramide errechnet sich wie der Flächeninhalt eines Quadrats: Länge mal Breite.
Merke
Berechnung der Grundfläche einer vierseitigen Pyramide mit der Seitenlänge $a$
$A_{Grundfläche} = a \cdot a = a^2$
Pyramide berechnen: Mantelfläche
Die Mantelfläche einer vierseitigen Pyramide besteht aus vier gleichschenkligen Dreiecken. Gleichschenklige Dreiecke sind Dreiecke mit zwei gleichlangen Seiten. Der Flächeninhalt gleichschenkliger Dreiecke errechnet sich wie folgt:
$A_{Dreieck} = \frac{1}{2} \cdot Grundseite \cdot Höhe = \frac{1}{2} \cdot a \cdot h_{Dreieck}$
Da die Mantelfläche aus insgesamt vier Dreiecken besteht, müssen wir den errechneten Flächeninhalt noch mit $4$ multiplizieren.
Merke
Berechnung der Mantelfläche
$A_{Mantel} = 4 \cdot (\frac{1}{2} \cdot a \cdot h_{Dreieck})$
Oberfläche einer Pyramide
Die Oberfläche einer Pyramide ist die Summe aus Grund- und Mantelfläche.
Merke
Berechnung der Oberfläche
$O_{Pyramide} =~Grundfläche~+~Mantelfläche~= a^2 + 4 \cdot (\frac{1}{2} \cdot a \cdot h_{Dreieck})$
Volumen einer Pyramide
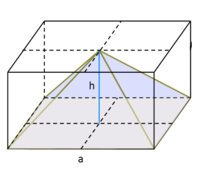
Die Formel zur Volumenberechnung einer Pyramide, in diesem Falle einer vierseitigen Pyramide, muss zunächst hergeleitet werden: In einen Würfel der Kantenlänge $a$ passen insgesamt sechs regelmäßige vierseitige Pyramiden, deren Seitenlänge ebenfalls $a$ beträgt.
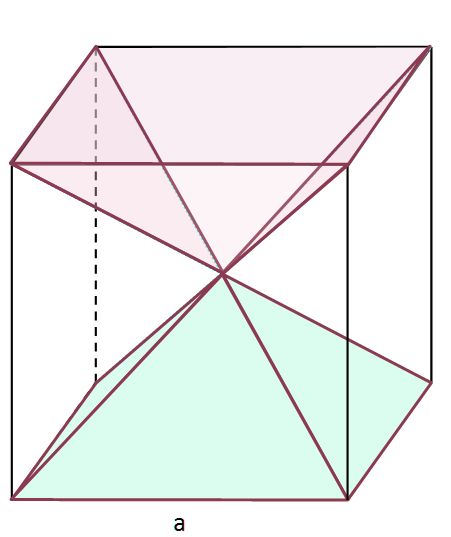
$6 \cdot V_{Pyramide} = V_{Würfel}$
Halbiert man den Würfel, erhält man ein Quader mit den Seitenlängen $a$ und der Höhe $h_{Pyramide}$. In diesen halbierten Würfel passen nur noch drei der Pyramiden.
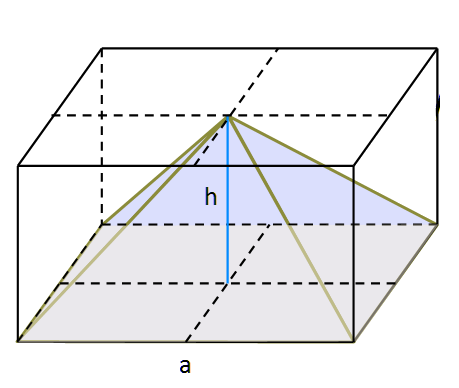
$3 \cdot V_{Pyramide} = \frac{1}{2} \cdot V_{Würfel} = V_{Quader}$
Das Volumen des Quaders können wir mit bekannten Größen ausdrücken:
$V_{Quader} = Länge~\cdot~Breite~\cdot~Höhe = a \cdot a \cdot h_{Pyramide}$
$3 \cdot V_{Pyramide} = a \cdot a \cdot h_{Pyramide}$
Die Gleichung lässt sich nach dem Volumen der Pyramide umstellen, indem wir durch $3$ teilen.
$V_{Pyramide} = \frac{1}{3} \cdot a \cdot a \cdot h_{Pyramide} = \frac{1}{3} \cdot a^2 \cdot h_{Pyramide}$
Merke
Volumen einer Pyramide
$V_{Pyramide} = \frac{1}{3} \cdot~Grundseite~ \cdot ~Höhe~$
$V_{Pyramide} = \frac{1}{3} \cdot a^2 \cdot h_{Pyramide}$
Teste dein neu erlerntes Wissen nun mit unseren Übungsaufgaben. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen! Übungsaufgaben
Du brauchst mehr Hilfe? Wir unterstützen Dich!
Bewertung bundesweit
Unsere Kunden über den Studienkreis Feedback von Eltern & Schüler:innen
Studienkreis Nachhilfe Deutschland:
4.60 / 5.00 Sterne bei 3700 Bewertungen
Weitere Erklärungen & Übungen zum Thema Mathematik > Geometrie
Klassenstufen in Mathematik
Weitere Fächer Lernen und Üben
Noch Fragen? Wir sind durchgehend für dich erreichbar
