Winkelfunktionen im nicht-rechtwinkligen Dreieck berechnen
Wenn du mit Dreiecken arbeitest kann es sein, dass du Aufgaben mit nicht rechtwinkligen Dreiecken bekommst. Hierfür gibt es ein paar einfache Tricks.
Methode
Wenn du kein rechtwinkliges Dreieck gegeben hast, musst du dir in dem Dreieck ein passendes rechtwinkliges Dreieck bilden bzw. suchen.
Mit den Winkelfunktionen darfst du ausschließlich im rechtwinkligen Dreieck rechnen. Die Begründung dafür ist ganz einfach! Um zum Beispiel mit dem Sinus rechnen zu können, brauchst du eine Hypotenuse und ohne rechten Winkel gibt es in dem Dreieck keine Hypotenuse. Auch wenn wir mit dem Tangens rechnen, brauchen wir eine Hypotenuse, da wir sonst die Ankathete des Winkels nicht eindeutig bestimmen können.
Die Dreiecke sind vor allem in Textaufgaben versteckt und du musst dir zuerst überlegen, wo das Dreieck ist. Dann überprüfst du, ob das Dreieck einen rechten Winkel hat. Wenn das nicht der Fall ist, musst du einen rechten Winkel bilden.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele zu Sin, Cos und Tan in nicht rechtwinkligen Dreiecken
Beispiel
Aufgabe 1:
Dieses Dreieck hat keinen rechten Winkel. Trotzdem möchten wir die Höhe des Dreiecks berechnen, also wie hoch der Punkt A über der Seite a liegt.
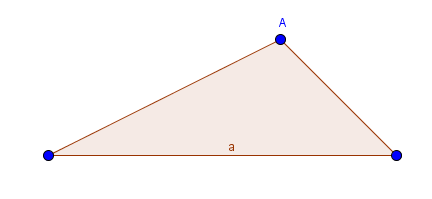
Dafür müssen wir in dem Dreieck einen rechten Winkel bilden, also legen wir eine Gerade senkrecht zu der Linie a bis zum Punkt A. Diese Gerade entspricht gleichzeitig auch unserer gesuchten Höhe.
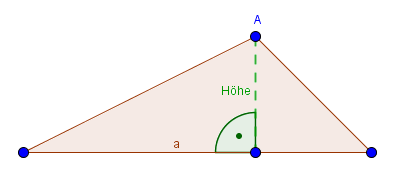
Nun können wir mit dem Sinus die Höhe berechnen. Dafür benötigen wir noch die Größe des Winkels $\beta$. Außerdem die Länge der Hypotenuse. Diese Angaben sind hier gegeben.
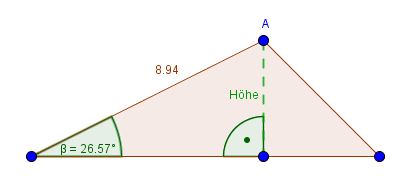
$Sinus(\beta) = \frac{Gegenkathete}{Hypotenuse}$
$sin(26,57^\circ) = \frac{Höhe}{8,94cm}$
$sin(26,57^\circ)\cdot{8,94cm} = Höhe$
${Höhe} \approx {4cm}$
Man hätte die Höhe auch mit dem Tangens berechnen können. Dafür müsste jedoch die Länge der Ankathete des Winkels $\beta$ gegeben sein.
Mit dem Kosinus können wir hier nicht arbeiten, da er das Verhältnis von Ankathete und Hypotenuse angibt, wir aber die Länge der Gegenkathete herausfinden müssen.
Die Aufgabe könntest du auch mit dem Satz des Pythagoras berechnen. Dafür würdest du nicht die Angabe des Winkels benötigen, sondern die beiden Längen der zwei Seiten im rechten Winkel. Sieh dir dazu die Seite vom Satz des Pythagoras an. Link: Satz des Pythagoras
Beispiel
Aufgabe 2:
Hierbei möchten wir wieder die Höhe des Punktes $C$ berechnen.
Gegeben ist die Länge der Seite $a = 8,06 cm$, die Länge der Seite $c = 9 cm$ und die Größe des Winkels $\beta$ = 119,72°.
Versuche erst einmal allein in das Dreieck einen rechten Winkel einzuzeichnen.
Nun haben wir unser rechtwinkliges Dreieck. Wie du siehst kann der Winkel auch außerhalb des Dreiecks liegen. Du solltest nur darauf achten, dass hier die Seite c die Länge zwischen Punkt A und B ist. Die Länge zwischen Punkt B und D ist nicht gegeben!
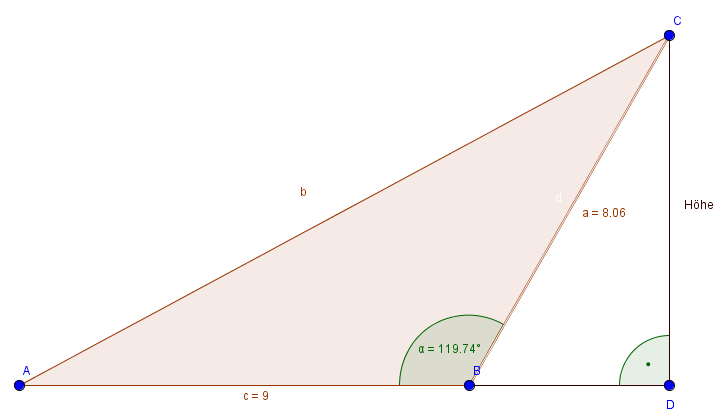
Nun können wir die Angabe $c = 9 cm$ nicht gebrauchen, weil es keine vollständige Kathete aus unserem rechtwinkligen Dreieck ist. Auch der Winkel $119,74^\circ$ liegt nicht in unserem Dreieck. Wir können jedoch mit ihm den Winkel auf der anderen Seite von B berechnen. Eine Gerade hat immer einen Winkel von $180^\circ$, wenn wir nun die $119,74^\circ$ davon abziehen erhalten wir ihn. Also ist $\gamma = 60,24^\circ $ groß.
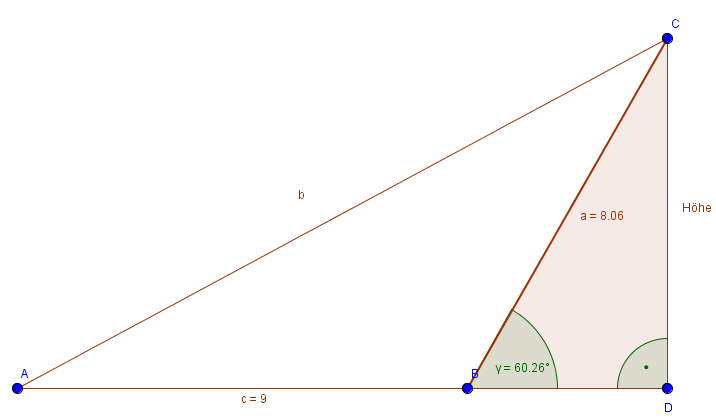
Wie du siehst haben wir einen Winkel und die Hypotenuse gegeben. Gesucht wird die Gegenkathete. Also rechnen wir mit dem Sinus.
$Sinus = \frac{Gegenkathete}{Hypotenuse}$
$sin(60,26^\circ) = \frac{Höhe}{8,06cm}$
${sin(60,26^\circ)}\cdot{8,06cm} = Höhe$
${Höhe} \approx {7cm}$
Textaufgabe und Lösung
Beispiel
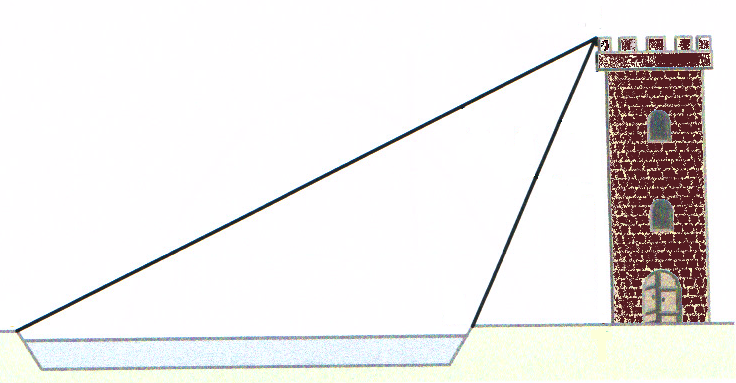
Hier sehen wir einen Turm, dessen Höhe wir bestimmen wollen. Neben dem Turm befindet sich ein See, der einen Durchmesser von 15 m hat. Der Winkel zwischen dem See und der Spitze des Turmes beträgt 30 Grad und die Länge der linken Seite des Sees bis zur Turmspitze beträgt 22 m.
Als erstes müssen wir nun wieder ein rechtwinkliges Dreieck einzeichnen, um eine der Winkelfunktionen anwenden zu können.
Wir zeichnen eine Gerade von der Spitze des Turms bis zum Boden. Damit haben wir unser rechtwinkliges Dreieck gebildet und auch eine Kathete, die der Höhe des Turms entspricht.
Nun zeichnen wir alle gegeben Längen ein.
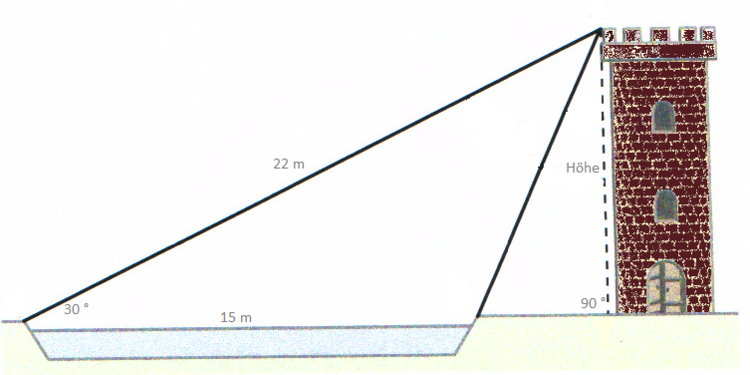
Jetzt fragst du dich sicher, welche der Angaben du benötigst. Die Breite des Sees (15 m) hilft uns nicht weiter, da sie sich auf das nicht rechtwinklige Dreieck bezieht. Also benötigen wir die Größe des Winkels ($30^\circ$) und die Länge der Hypotenuse ($22 m$). Überlege mit welcher Winkelfunktion du rechnen möchtest.
Wir suchen die Gegenkathete von $30^\circ$ und haben die Hypotenuse gegeben. Also rechnen wir mit dem Sinus.
$sin(30^\circ) = \frac{Gegenkathete}{Hypotenuse}$
$sin(30^\circ) = \frac{Höhe}{22m}$
$sin(30^\circ) \cdot 22m = 11m$
Der Turm ist $11 m $ hoch.
Jetzt weißt du, wie du die Winkelfunktionen auf Dreiecke anwenden kannst, die nicht rechtwinklig sind. Dein neues Wissen kannst du nun in unseren Übungen austesten. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
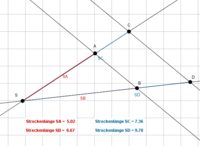
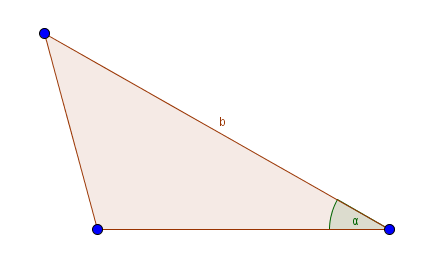
In welches der vier Dreiecke wurde der rechte Winkel richtig eingezeichnet, um die Länge der Seite b zu berechnen?
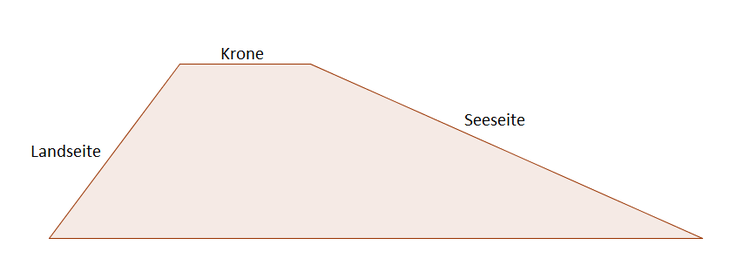
Wir haben einen Deich gegeben, von dem die gesamte Breite ermittelt werden soll. Die Krone des Deiches ist $3 m$ lang und $4 m$ hoch. Zur Seeseite beträgt der Winkel $\alpha = 24^\circ$ und zur Landseite $\beta = 53^\circ$.
Berechne nun die Breite des Deiches.
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
