Winkelfunktionen in rechtwinkligen Dreiecken
Trigonometrie ist ein Teilbereich der Geometrie, bei dem es um Dreiecke geht. Man unterscheidet hier zwischen rechtwinkligen und gewöhnlichen (nicht rechtwinkligen) Dreiecken. Wir beschäftigen uns hier zunächst nur mit den rechtwinkligen Dreiecken.
Für Berechnungen an rechtwinkligen Dreiecken sind die Winkelfunktionen wichtig. Man unterscheidet drei Winkelfunktionen: Sinus, Kosinus und Tangens.
Rechtwinkliges Dreieck - Katheten bestimmen
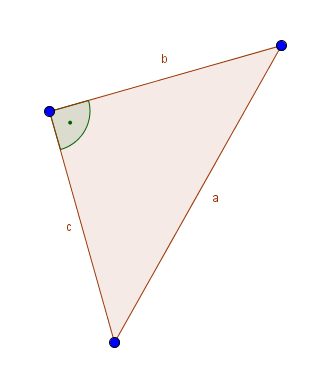
Ein rechtwinkliges Dreieck zeichnet sich dadurch aus, dass es einen rechten Winkel hat. Wenn zwei Seiten senkrecht aufeinander stehen, bilden sie einen rechten Winkel. In Zeichnungen wird ein rechter Winkel durch einen Punkt gekennzeichnet.
Gut zu wissen
Hinweis
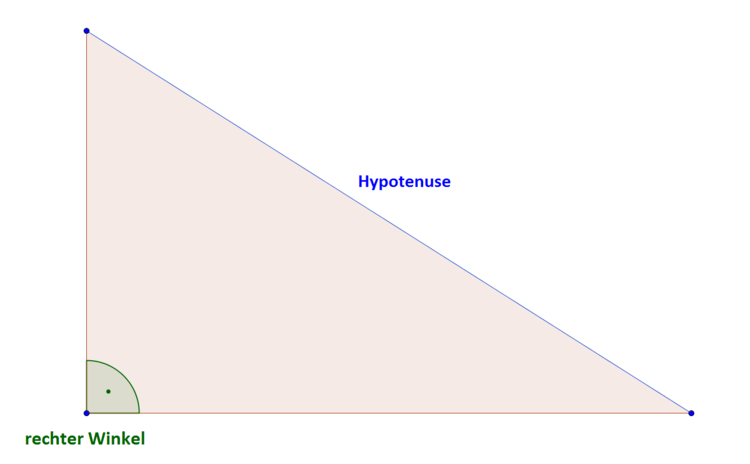
Die Hypotenuse liegt immer gegenüber vom rechten Winkel (90°).
Merke
Merke
Sinus, Kosinus und Tangens darfst du nur im rechtwinkligen Dreieck anwenden.
Die Seiten, die den rechten Winkel einschließen, werden Katheten genannt.
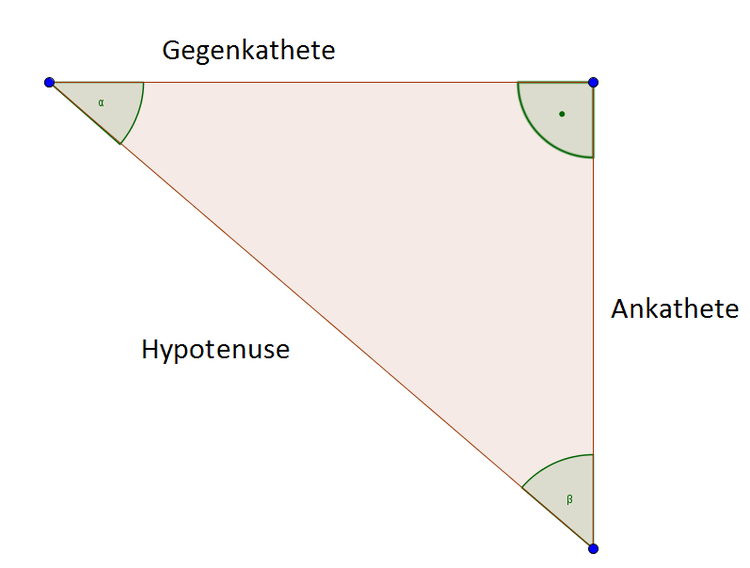
Des Weiteren unterscheidet man zwischen Ankathete und Gegenkathete. Je nachdem, von welchem Winkel aus du das Dreieck betrachtest, wird eine Kathete als Ankathete und die andere als Gegenkathete bezeichnet. Die Benennung der Katheten bezieht sich also immer auf einen Winkel.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Ankathete und Gegenkathete
Gut zu wissen
Hinweis
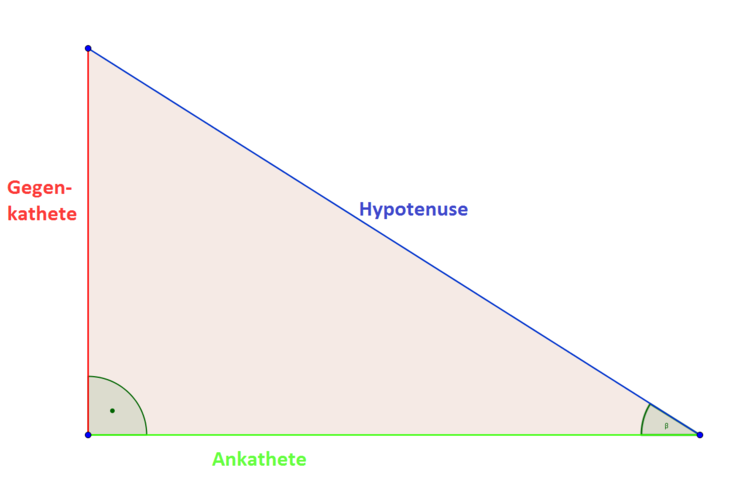
Die Ankathete ist die Seite, an die der Winkel (hier $\beta$) anliegt. Wie du an unserem Dreieck siehst, wird der Winkel $\beta$ aus zwei Seiten gebildet: aus der Hypotenuse und aus der Ankathete. Du musst darauf achten, die Hypotenuse (immer gegenüber vom rechten Winkel) nicht mit der Ankathete zu verwechseln. Nun bleibt nur noch zu klären, welche Seite die Gegenkathete ist. Die Gegenkathete liegt immer gegenüber vom gegebenen Winkel.
Merke
Merke
Die Ankathete ist die Seite, die an den gegebenen Winkel angrenzt und nicht die Hypotenuse ist.
Die Gegenkathete ist die Kathete, die dem gegebenen Winkel gegenüber liegt.
Vertiefung
Symbole für Winkel
Winkel werden mit griechischen Buchstaben benannt.
$\alpha$ (alpha), $\beta$ (beta) und $\gamma$ (gamma) sind die am häufigsten verwendeten.
Entweder ist die Gradzahl gegeben oder du musst die Gradzahl, mit Hilfe der Winkelfunktionen, berechnen.
Jetzt hast du das nötige Vorwissen, um zu lernen, wann und wie du die drei Winkelfunktionen, Sinus, Kosinus und Tangens, anwenden kannst.
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang