In der Mathematik gibt es viele Figuren. Wenn wir Figuren miteinander vergleichen, sehen sich manche Figuren sehr ähnlich, manche sind sogar identisch und wieder andere sehen sehr unterschiedlich aus. Wenn wir nun zwei Figuren miteinander vergleichen, können wir bestimmen, ob eine mathematische Symmetrie vorliegt, das heißt, ob die Figuren symmetrisch zueinander sind. In diesem Lerntext erhältst du einen Überblick über alle Symmetriearten, die man in der Mathematik kennt.
In der Geometrie gibt es genau drei Arten von Symmetrien.
Achsensymmetrie
Als erstes widmen wir uns der Achsensymmetrie. Eine Figur wird an einer Achse gespiegelt, daher der Begriff Achsensymmetrie.
Wenn wir eine Figur oder einen Körper an einer Achse spiegeln, dann wird alles, also jeder Punkt, jede Linie und jeder Winkel an dieser Achse gespiegelt. Die Vorgehensweise ist jedoch recht einfach: Wenn du eine Figur an einer Achse spiegeln möchtest, brauchst du nur die Eckpunkte deiner Figur an der Spiegelachse zu spiegeln. Nachdem du alle Punkte gespiegelt hast, kannst du die Bildpunkte (die gespiegelten Punkte) einfach miteinander verbinden und erhältst so deine gespiegelte Figur (siehe Abbildung).
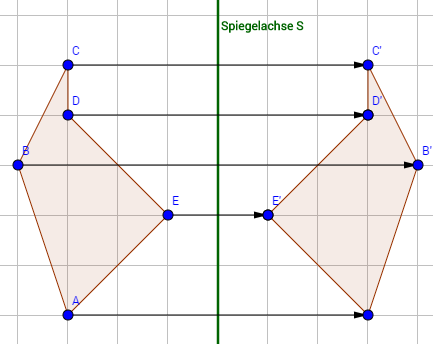
Merke
Achsensymmetrische Figuren haben immer den gleichen Abstand von der Symmetrieachse. Sie sind zudem gespiegelt.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Punktsymmetrie
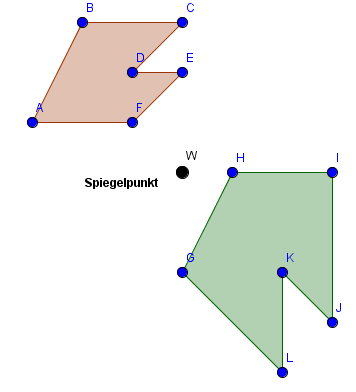
Als zweites widmen wir uns nun der Punktsymmetrie bzw. der Punktspiegelung. Die Figur wird nun an einem Punkt gespiegelt (siehe Abbildung). So entsteht eine gedrehte Kopie der Originalfigur. Die Vorgehensweise ist ähnlich wie bei der Achsenspiegelung: Du spiegelst nacheinander alle Eckpunkte deiner Figur an dem Spiegelpunkt. Nachdem du alle Eckpunkte gespiegelt hast, kannst du die Bildpunkte verbinden. Du erhältst die Bildfigur (siehe Abbildung).
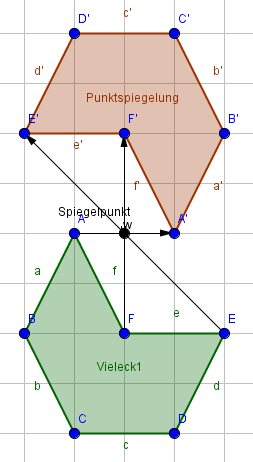
Punktsymmetrische Figuren werden an einem bestimmten Punkt gespiegelt, dem Symmetriezentrum, auch Spiegelpunkt genannt. Dieser Punkt kann auch ein Eckpunkt des Vielecks sein.
Der Abstand zwischen Bildpunkt und Spiegelpunkt ist immer genauso groß wie der Abstand zwischen Punkt und Spiegelpunkt. Oder anders ausgedrückt: Punkt und Bildpunkt sind Anfangs- und Endpunkt einer Strecke. Der Spiegelpunkt liegt immer in der Mitte dieser Strecke.
Merke
Die gespiegelte Strecke ist immer genauso lang wie die Originalstrecke.
Es gilt: $\overline{E'W} = \overline{EW}$, $\overline{F'W} = \overline{FW}$, $\overline{D'W} = \overline{DW}$,...
Rotationssymmetrie
Die dritte Art der Symmetrie ist die Rotationssymmetrie. Bei der Rotationssymmetrie wird die Figur um den Spiegelpunkt gedreht. Der Rotationswinkel gibt dabei an, um wie viel Grad die Figur um den Spiegelpunkt gedreht wird. Der Spiegelpunkt kann ein Punkt der Figur sein. In der Abbildung ist der Spiegelpunkt der Punkt $A$. Die Figur wurde nun einmal an diesem Punkt gespiegelt (dunkelgrüne Bildfigur) und einmal an diesem Punkt um 80° gedreht (hellgrüne Bildfigur). Eine Punktspiegelung entspricht einer Drehung um 180°. Somit ist die Punktspiegelung ein Sonderfall der Rotationsspiegelung.
Merke
Bei der Rotationsspiegelung werden Figuren um einen Spiegelpunkt gedreht. Der Spiegelpunkt kann ein Punkt der Figur sein.
Asymmetrie
Zuletzt gibt es die Asymmetrie. Wenn zwei Figuren weder achsensymmetrisch noch punktsymmetrisch zueinander sind und auch nicht durch eine Rotationsspiegelung ineinander überführt werden können, dann sind diese beiden Figuren asymmetrisch.
Merke
Asymmetrische Figuren können durch keine Art der Spiegelung ineinander überführt werden.
Gut zu wissen
Genauso wie in der Mathematik gibt es auch in der deutschen Sprache symmetrische Wörter oder Sätze. Ein Beispiel dafür ist der Satz: "Dreh mal am Herd." Dieser Satz, im deutschen Palindrom genannt, kann vorwärts wie rückwärts gelesen werden (unter der Bedingung, dass die Leerzeichen etwas versetzt werden).
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Übungsaufgaben
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Weitere Erklärungen & Übungen zum Thema
Mathematik
> Geometrie
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
