Zentrische Streckung - Einführung & Erklärung
Teil der Mathematik ist die Zentrische Streckung. In diesem Lerntext erhältst du zur Zentrischen Streckung eine Erklärung. Bereits im Lerntext Wie lauten die Kongruenzsätze wurde die Zentrische Streckung behandelt. Dort haben wir Dreiecke, die vergrößert oder verkleinert wurden, behandelt. Doch wie genau eine Figur verkleinert oder vergrößert werden kann, haben wir noch nicht besprochen. Die Anwendung der Zentrischen Streckung erklären wir dir jetzt. Am Ende des Lerntextes findest du zur Zentrischen Streckung Aufgaben mit Lösungen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Die Zentrische Streckung: Erklärung
Die Zentrische Streckung hat mit dem Strecken einer Figur zu tun. Dies passiert bei vielen Prozessen im Computer automatisch. Wenn du zum Beispiel diese Webseite aufrufst, passt dein Browser diese Webseite automatisch auf die Größe deines Bildschirmes an, damit du nicht etwa einen schwarzen Balken am Rand hast oder nur einen Teil des Textes sehen kannst. Dieses Phänomen können wir mathematisch beschreiben.
Figuren werden bei der Zentrischen Streckung vergrößert oder verkleinert, wobei die Verhältnisse der einzelnen Längen und Strecken zueinander beibehalten werden. Ausgangspunkt der Streckung ist ein bestimmter Punkt, das sogenannte Streckungszentrum.
Merke
Merke
Bei der Zentrischen Streckung werden Figuren vergrößert oder verkleinert, wobei die Seitenverhältnisse unverändert bleiben. Ausgangspunkt ist das Streckungszentrum.
Beispiel
Beispiel
Verdeutlichen wir die Zentrische Streckung an einem Dreieck als Beispiel:
Bauarbeiter sollen einen Weg mit Dreiecken verzieren. Das Muster besteht abwechselnd aus kleinen und großen Dreiecken. Dabei sind die großen Dreiecke immer genau doppelt so groß wie die kleinen Dreiecke. Das Muster soll bis zum Ende des Weges fortgesetzt werden.
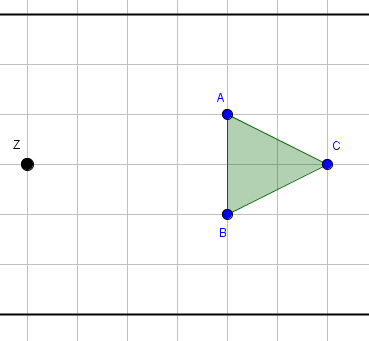
Die Ausgangsfigur ist dieses Dreieck. Auf dieses Dreieck soll nun ein doppelt so großes Dreieck folgen. Wir müssen das abgebildete Dreieck also vergrößern.
Wir zeichnen zuerst eine Halbgerade vom Streckungszentrum $Z$ durch die Punkte $A$, $B$ und $C$.
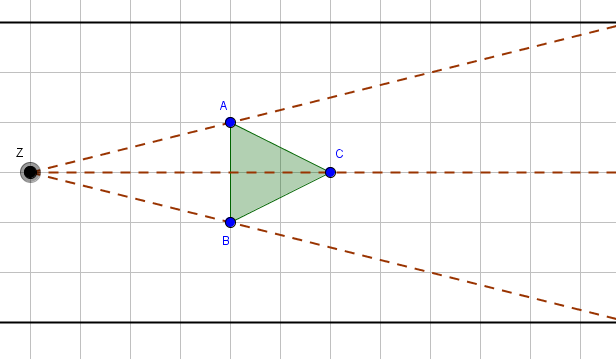
Jetzt müssen wir ein wenig rechnen. In der Aufgabenstellung steht, dass das zweite Dreieck genau doppelt so groß sein soll wie das erste Dreieck. Der Streckungsfaktor beträgt also $2$. Der Abstand vom Streckungszentrum $Z$ zum Punkt $C$ beträgt $6~ cm$. Da der Streckungsfaktor $2$ beträgt, muss der Abstand von $Z$ zu $C'$ $12~cm$ betragen ($2 \cdot 6~cm=12~cm$). Analog werden die Punkte $A'$ und $B'$ gefunden. Das heißt, du musst zuerst die Längen der Abstände von $Z$ zu $A$ und von $Z$ zu $B$ messen und diese dann verdoppeln.
Es ergibt sich:
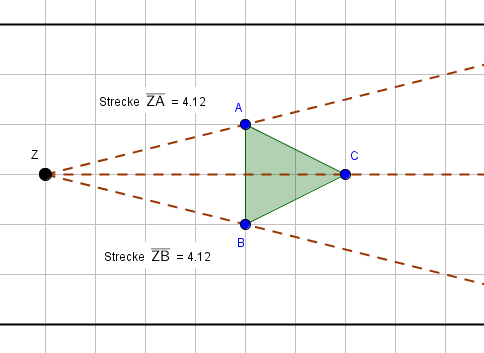
$\overline{ZA}= 4,12~cm~~\rightarrow~~\overline{ZA'} = 2 \cdot 4,12~cm = 8,24~cm$
Jetzt zeichnen wir die jeweiligen Bildpunkte ein und erhalten so das Grundgerüst des vergrößerten Dreiecks.
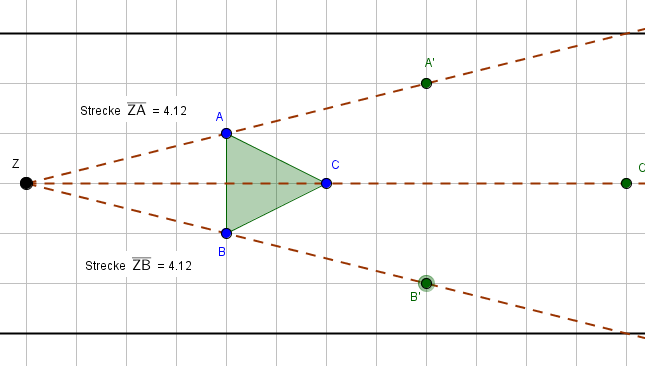
Nun verbinden wir die Bildpunkte und erhalten so das gestreckte/vergrößerte Dreieck.
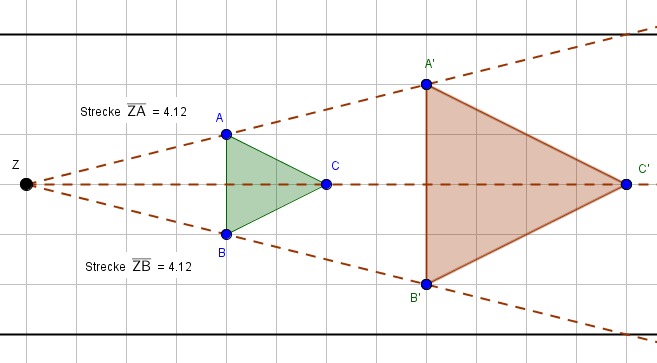
Der Streckungsfaktor kann auch negativ sein. Der Streckungsfaktor wird also zunächst immer kleiner, bis er den Wert $0$ erreicht. Ist der Streckungsfaktor $0$, werden alle Punkte im Streckungszentrum abgebildet, so dass die Bildfigur aus einem einzigen Punkt besteht, dem Streckungszentrum. Wenn der Streckungsfaktor nun noch kleiner wird, also negativ, werden die Punkte am Streckungszentrum gespiegelt. Die Bildfigur entsteht dann auf der anderen Seite des Streckungszentrums.
Zentrische Streckung - Zirkelzeichnung
Man kann eine Streckung auch mit dem Zirkel anfertigen. Wir müssen um den jeweiligen Punkt (im Bild Punkt $A$) einen Kreis so schlagen, dass $Z$ auf dem Kreis liegt. Dort, wo die Hilfsgerade den Kreis schneidet, liegt der gespiegelte Punkt $A'$. Dies funktioniert natürlich nur, wenn der Streckungsfaktor $2$ beträgt. Bei anderen Streckungsfaktoren ändert sich die Anzahl der zu zeichnenden Kreise. So muss man bei einer Streckung mit dem Faktor $3$ zwei Kreise zeichnen (Punkt $A''$ wäre in diesem Fall der gesuchte Bildpunkt) etc.
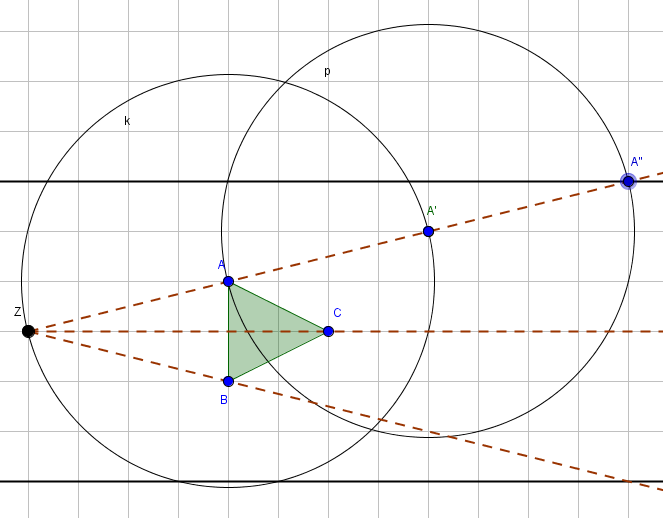
Flächeninhalt von zentrisch gestreckten Figuren
Für den Flächeninhalt einer gestreckten Figur gibt es eine einfache Regel: Der Flächeninhalt der Originalfigur wird mit dem Faktor $\bf{k^2}$ multipliziert.
Merke
Merke
Der Flächeninhalt der gestreckten Figur ist genau das k²-fache des Originalflächeninhaltes, also:
$\mathbf{A_{gestreckt} = A_{original} \cdot k^2}$
Zur Vertiefung dieses Themas schau auch noch einmal in die Aufgaben! Viel Spaß und Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang