Wie lauten die Kongruenzsätze?
In diesem Lerntext beschäftigen wir uns mit den sogenannten Kongruenzsätzen. Doch was bedeutet Kongruenz zunächst überhaupt?
Kongruenz von Figuren
Im Alltag treffen wir oft auf Gegenstände oder Personen, die sich ähnlich sind, wie etwa Zwillinge oder Häuser. Dieses Phänomen können wir auch in der Mathematik beobachten. Hier können Figuren ähnlich bzw. kongruent zueinander sein, so wie in dem ersten Bild. Hier sind die beiden Dreiecke kongruent zueinander.
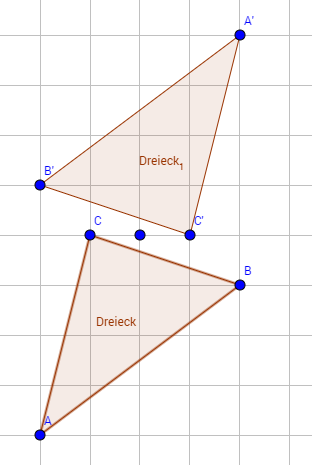
Das eine Dreieck ist einfach nur eine Spiegelung des anderen und hat genau dieselben Winkel und Seitenlängen. Es lässt sich problemlos in das andere Dreieck "drehen".
Merke
Objekte nennt man kongruent, wenn sie gleiche Seitenlängen und Winkel haben. Kongruente Objekte lassen sich exakt aufeinander abbilden.
Hierbei ist es nicht wichtig, ob der Gegenstand ein Dreieck, ein Viereck oder anderes Vieleck oder wie er gedreht ist. Solange die Längen der Seiten und die Winkel übereinstimmen, sind sie kongruent.
Kongruenzsätze bei Dreiecken
In speziellen Fällen, wie etwa bei Dreiecken, kann man Merksätze bilden, um die Kongruenz der beiden Dreiecke leichter und ohne großes Rechnen zu ermitteln.
1. Kongruenzsatz: -SSS- Zwei Dreiecke sind zueinander kongruent, wenn sie in allen drei Seiten übereinstimmen.
Man versteht darunter also, dass bei identischen Seitenlängen der Dreiecke, beide Dreiecke kongruent sind.
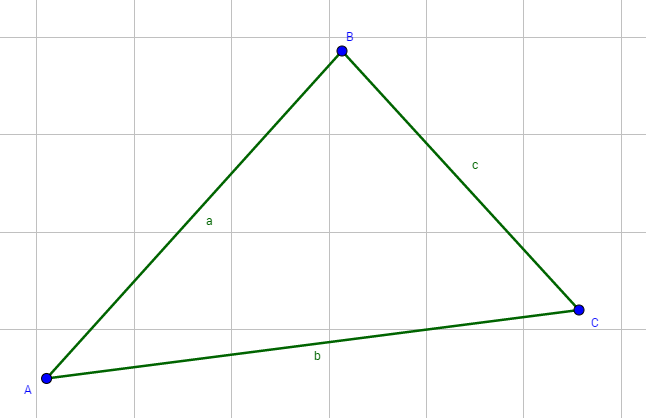
2. Kongruenzsatz: -SWS- Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen.
Hier ist gemeint, dass beim gegebenen Dreieck ein Winkel und die zwei Seiten am Winkel kongruent sind. Der Winkel wird dann eingeschlossener Winkel genannt.
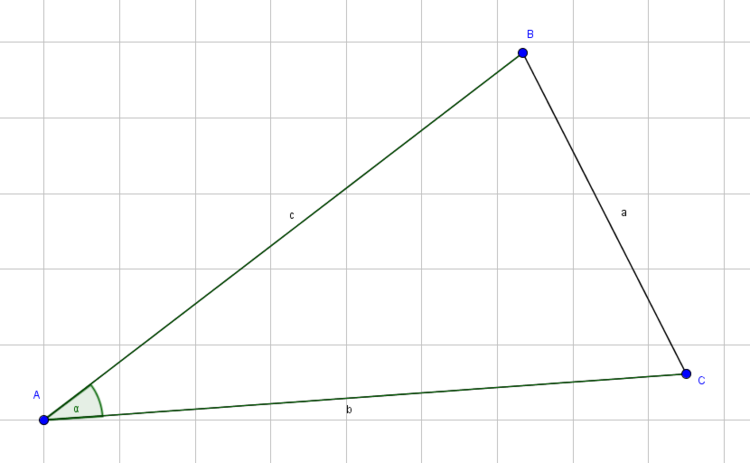
3. Kongruenzsatz: -WSW- Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Winkeln und der eingeschlossenen Seite übereinstimmen.
Ähnliches wie die anderen Kongruenzsätze sagt auch dieser aus. So sind zwei Dreiecke kongruent zueinander, wenn zwei Winkel und die eingeschlossene Seite bei beiden kongruent sind.
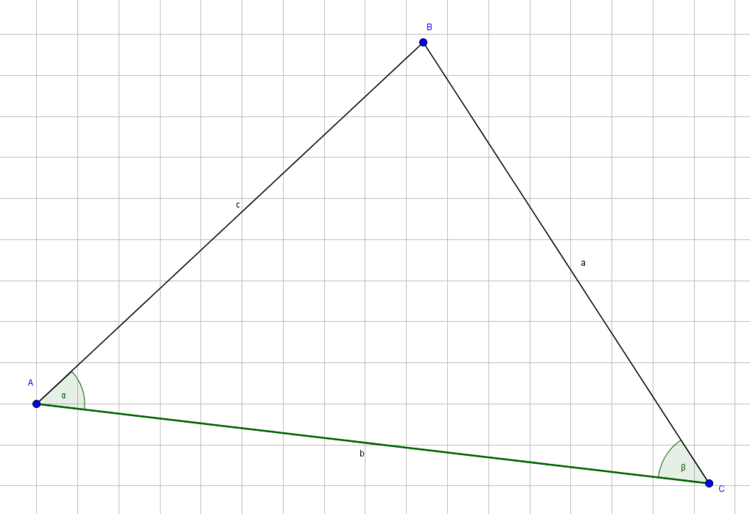
4. Kongruenzsatz: -SSW- Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel übereinstimmen.
Im letzten Satz wird gesagt, dass zwei Seiten und der größte Winkel übereinstimmen müssen. Der Winkel ist hierbei immer in seiner Position gegenüber der längsten Seite des Dreiecks.

- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Ähnlichkeit von Figuren
Neben der Kongruenz von Figuren gibt es auch die Ähnlichkeit von Figuren. Anders als bei der Kongruenz müssen hierbei die Seitenlängen nicht gleich sein. Die Winkel sind jedoch auch bei ähnlichen Figuren gleich.
Merke
Ähnliche Abbildungen haben immer dieselben Winkel und dieselbe Form.
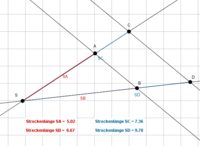
Ein Spezialfall der Ähnlichkeit von Figuren ist die zentrische Streckung Hierbei ist die Figur, wie in dem interaktiven Arbeitsblatt, an einem bestimmten Punkt gestreckt. Diese Streckung wird in einem Faktor dargestellt, dem Faktor k oder auch Streckungsfaktor genannt. Wenn also ein Dreieck doppelt so groß wie ein anderes ist, so muss der Faktor k gleich 2 sein. Um zu sehen, ob die Objekte ähnlich sind, benötigen wir also die Formel:
Merke
$\overline {AB} = \overline {A'B'} * k$
Hierbei steht die Angabe $\overline {AB}$ für die Länge der Seite zwischen den Punkten A und B und die Angabe $\overline {A'B'}$ für den Abstand zwischen den Punkten A' und B'. k gibt den Streckungsfaktor an.
Wenn eine der Angaben nicht gegeben ist, kann man selbstverständlich auch mit dem Flächeninhalt die fehlenden Seitenlängen herausfinden. Es gilt, dass der Flächeninhalt des entstehenden Dreiecks genau k²-Mal der Flächeninhalt des Originaldreiecks ist.
Es gilt also die folgende Formel:
Merke
A' = A * k²
Methode
Interaktives Arbeitsblatt:
Schauen wir uns doch mal die Ähnlichkeit von Figuren in GeoGebra an. Du kannst den Schieberegler mit dem Streckungsfaktor k verändern, um das zweite Dreieck anzupassen und so das Gelernte anzuwenden.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema