Strahlensätze - Aufgaben mit Lösungen
Im Lerntext zum Thema Strahlensätze haben wir die Formel des 1. Strahlensatzes und 2. Strahlensatzes kennengelernt. Wir haben gelernt, unter welchen Voraussetzungen wir die jeweiligen Strahlensätze anwenden können und wie wir die Gleichungen aufstellen müssen. In diesem Lerntext wollen wir dir nun zeigen, wo und wie du die Strahlensätze im Alltag anwenden kannst. Du bekommst also hier zum Thema Strahlensätze Aufgaben mit Lösungen. Wir betrachten daher nun zwei Beispiele aus dem Alltag.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Strahlensatz: Aufgabe 1
Beispiel
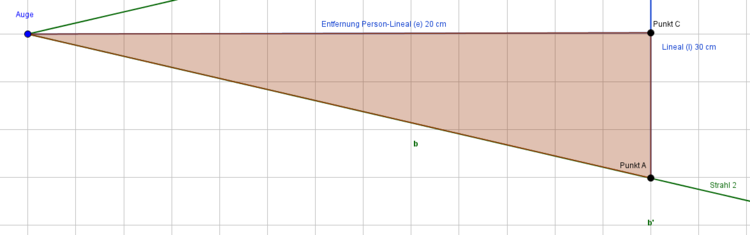
Aufgabenstellung: Ein großer Baum soll gefällt werden. Dieser steht ca. 8 Meter von einem Haus entfernt. Die Frage ist nun, ob der Baum das Haus treffen könnte, wenn er umfällt. Als Hilfsmittel nutzen wir ein 30 cm langes Lineal, das wir in einem Abstand von 20 cm vor unser Auge halten. Ferner wissen wir, dass die Entfernung vom Auge zur Wurzel des Baumes ca. 8 Meter beträgt. Du kannst nun berechnen, ob der Baum beim Fallen das Haus beschädigen kann.
Herangehensweise:
Wir machen eine Skizze und überlegen, welche Größe gesucht und welche Größen gegeben sind. Wir stehen vor einem Baum, dessen Höhe wir ermitteln sollen. Somit ist die Strecke zwischen Punkt E und Punkt F gesucht.
Wir wissen, dass wir das Lineal genau 20 cm von uns entfernt in der Hand halten. Weiter wissen wir, dass das Lineal genau 30 cm lang ist. Und wir kennen auch den Abstand vom Auge zur Baumwurzel, der ca. 8 Meter beträgt. In einer Skizze zusammengetragen, ergibt sich folgendes Bild:
Wir erkennen, dass wir den zweiten Strahlensatz zur Berechnung der unbekannten Länge benutzen müssen. Wir stellen den zweiten Strahlensatz wie folgt auf:
$\large{\frac{b}{b'} = \frac{l}{x}}$
Wir setzen die bekannten Werte ein. Daraus ergibt sich:
$\large{\frac{b}{8~m} = \frac{30~cm}{x}}$
Um die Länge der Seite $x$ berechnen zu können, fehlt uns nun leider noch die Länge der Seite $b$. Wir gucken nun nochmals genau auf die Skizze und stellen fest, dass wir die Länge der Seite $b$ mithilfe des Satz des Pythagoras berechnen können. Die Seite $b$ ist die Hypotenuse in einem rechtwinkligen Dreieck. Es gilt:
$\large{b^2 = e^2 + (\frac{1}{2}\cdot l)^2}$
Wir setzen nun die Werte, die wir kennen, ein und erhalten dann:
$\large{b^2 = 20^2 + 15^2}$
$\large{b^2 = 625}$
$\large{b_1 = 25}$ und $\large{b_2 = -25}$
Das negative Ergebnis macht hier keinen Sinn, da eine Länge keinen negativen Wert annehmen kann. Wir können $b=-25$ demnach ausschließen. Die Länge der Strecke $b$ beträgt also $25$ Meter. Diesen Wert setzen wir nun in die Strahlensatz-Formel ein. Wir erhalten:
$\Large{\frac{25 ~cm}{800~ cm} = \frac{30 ~cm}{x}}$
Auf der linken Seite der Gleichung können wir die $cm$ kürzen. Nun bilden wir das Kreuzprodukt, um die Brüche aufzulösen. Wir erhalten:
$ 25 \cdot x = 800 \cdot 30~cm$
Mithilfe einer einfachen Äquivalenzumformung können wir $x$ nun berechnen und erhalten dann:
$ x = 960~cm$
Die Höhe des Baumes beträgt ca. $9,6$ Meter. Es besteht daher die Gefahr, dass der Baum im Fall das Haus trifft.
Strahlensatz: Aufgabe 2
Beispiel
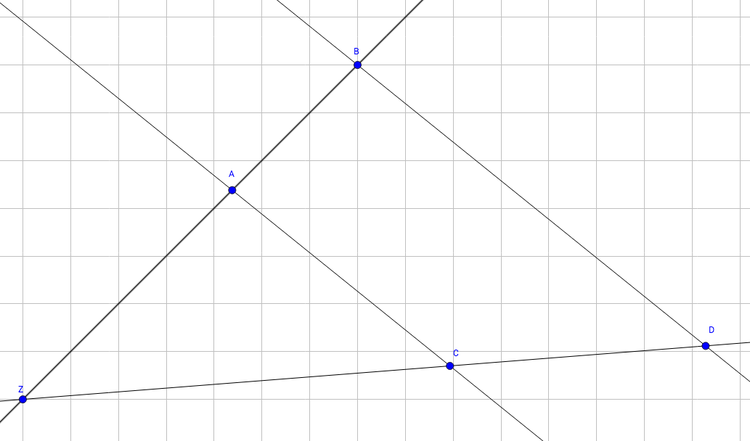
Es soll eine Seilbahn über einen See gebaut werden. Daher muss die Breite des Sees an einer bestimmten Stelle ermittelt werden, nämlich zwischen Punkt $A$ und Punkt $B$. Versuche, die Breite des Sees zwischen $A$ und $B$ mithilfe der gegebenen Werte zu berechnen.
Zunächst fertigen wir eine Skizze an und tragen die gegebenen Werte ein. Da die Längen der Parallelen beide nicht bekannt sind, können wir nur den ersten Strahlensatz anwenden. Am geschicktesten ist es, den Strahlensatz so aufzustellen, dass die gesuchte Größe im Zähler eines Bruches steht:
$\large{\frac{x}{160~m} = \frac{960~m}{300~m}}$
Auf der rechten Seite können wir die Einheit $Meter$ kürzen. Danach multiplizieren wir über Kreuz, um den Bruch zu beseitigen. Wir erhalten:
$\large{x\cdot 300= 960\cdot 160~m}$
Nach einer einfachen Äquivalenzumformung erhalten wir:$\large{x=512~Meter}$
Die Breite des Sees zwischen $A$ und $B$ beträgt ca. $512$ Meter.
Nun konntest du sicher nochmal mehr zum Thema Strahlensätze anhand der Anwendungsaufgaben verstehen. Zur Vertiefung schau auch noch einmal in die Übungen zum Strahlensatz! Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
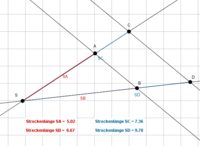
Berechne die Länge der Strecke $\overline{ZA}~$.
Es gilt:
$\overline{ZB}~$ = 100 cm,
$\overline{ZC}~$ = 35 cm und
$\overline{ZD}~$ = 175 cm
.
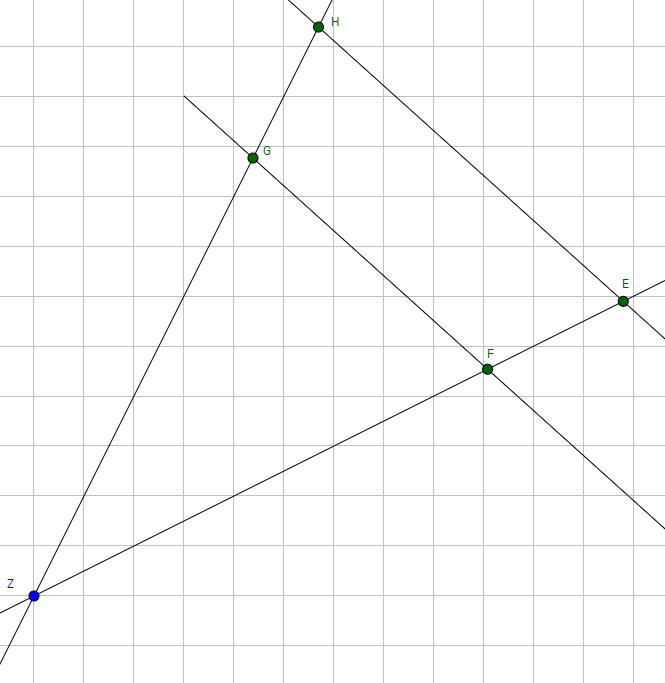
Berechne mithilfe eines Strahlensatzes die Länge der Strecke $\overline{FG}$. Es gilt:
$\overline{HE}$ = 400 m,
$\overline{HG}$ = 50 m und
$\overline{ZG}$ = 150 m
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
