Winkelfunktionen: Textaufgabe mit Lösung
Spätestens in der 10. Klasse werden dir in der Geometrie Winkelfunktionen in Form von Textaufgaben begegnen. In diesem Lerntext wird eine Textaufgabe zum Thema Winkelfunktionen gelöst. Dabei wird im Detail auf die Vorgehensweise beim Lösen von solchen Textaufgaben eingegangen.
Lösen von Textaufgaben - Vorgehensweise
Methode
Methode
- Suche das Dreieck und markiere den rechten Winkel.
- Was ist gesucht und was ist gegeben? Markiere dir dies in einer kleinen Skizze.
- Benenne die Seiten des Dreiecks (Gegenkathete, Ankathete und Hypotenuse).
- Mithilfe der Skizze kannst du nun überlegen, mit welcher Winkelfunktion du arbeiten kannst.
- Als Letztes musst du nur noch die Angaben in die Winkelfunktion einsetzen, eventuell ein wenig umstellen, und dann die gesuchte Größe berechnen.
Textaufgabe Winkelfunktionen
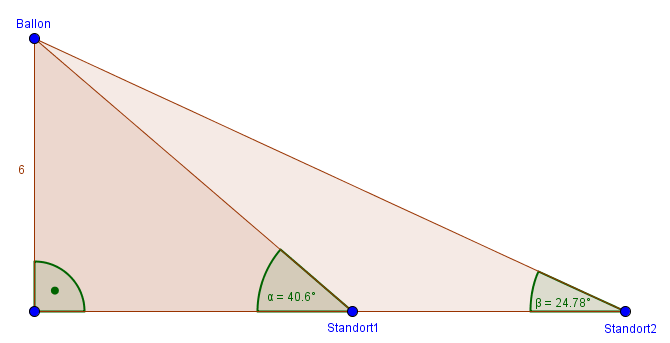
Ein Mädchen (Standort 1) hat von seiner Oma (Standort 2) einen Ballon geschenkt bekommen. Das Mädchen lässt den Ballon versehentlich los und nun schwebt er 6 m über dem Boden. Wie weit sind die Oma und das Mädchen voneinander entfernt?
Gucke dir das Bild genau an, ergänze fehlende Angaben soweit wie möglich und versuche dann, die Entfernung zwischen Oma und Mädchen mithilfe einer Winkelfunktion zu berechnen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Lösungsweg der Textaufgabe
Wie berechnen wir nun den Abstand zwischen dem Mädchen und seiner Oma? Wir haben, wie du in der unteren Zeichnung siehst, zwei Dreiecke gegeben. In dem kleineren Dreieck ist die Ankathete des Winkels $\alpha$ der Abstand zwischen dem Mädchen und dem Punkt auf dem Boden unter dem Ballon. In dem größeren Dreieck ist die Ankathete des Winkels $\beta$ die Länge des Abstandes zwischen der Oma und dem Punkt auf dem Boden unter dem Ballon. Wenn wir nun diese beiden Längen berechnen und danach die beiden Längen voneinander subtrahieren, haben wir den Abstand zwischen Oma und Mädchen.
$\rightarrow$ Abstand zwischen Oma und Mädchen = (Länge von dem Punkt auf dem Boden unter dem Ballon bis zur Oma) - (Länge von dem Punkt auf dem Boden bis zum Mädchen)
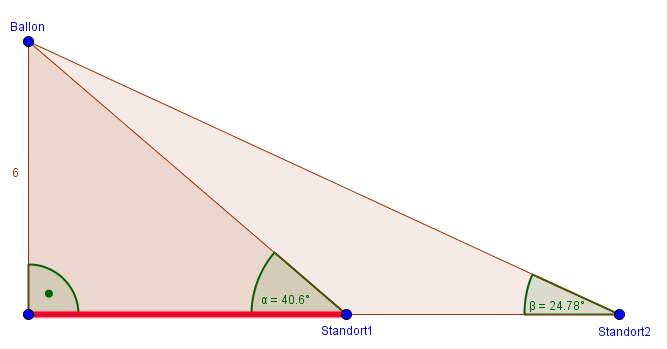
Wie berechnen wir nun die Länge des Abstandes zwischen dem Mädchen und dem Punkt auf dem Boden unter dem Ballon? Wir betrachten das Dreieck vom Winkel $\alpha$ aus. Wir kennen die Länge der Gegenkathete und suchen die Länge der Ankathete. Somit sind wir beim Tangens, denn nur in der Winkelfunktion Tangens kommen Gegenkathete und Ankathete vor.
Gut zu wissen
Hinweis
Zur Vertiefung der Winkelfunktionen schaue unbedingt in den Lerntexten zu den drei Winkelfunktionen Sinus, Kosinus und Tangens rein. Dort findest du auch jeweils zu allen drei Winkelfunktionen Aufgaben zum Nachvollziehen dieses Themas.
$\alpha = 40,6 ^\circ; Gegenkathete = 6~m; Ankathete =~?$
$tan(\alpha) = \frac{Gegenkathete}{Ankathete}$
$tan(40,6 ^\circ) = \frac{6~m}{Ankathete}$
${tan(40,6 ^\circ)}\cdot{Ankathete} = 6~m$
$Ankathete = \frac{6~m}{tan(40,6 ^\circ)}$
${x} \approx {7~m}$
Der Abstand zwischen dem Mädchen und dem Punkt auf dem Boden unter dem Ballon beträgt also ungefähr $7$ Meter.
Uns fehlt nun noch der Abstand zwischen dem Punkt auf dem Boden unter dem Ballon und der Oma. Diesen Abstand können wir analog berechnen.
Wir kennen $\beta$ und die Länge der Gegenkathete zu $\beta$. Gesucht ist die Länge der Ankathete zu $\beta$.
$\beta= 24,78^\circ; Gegenkathete = 6~m, Ankathete =~?$
$tan(\beta) = \frac{Gegenkathete}{Ankathete}$
$tan(24,78^\circ) = \frac{6~m}{Ankathete}$
${tan(24,78^\circ)}\cdot{Ankathete} = 6~m$
$Ankathete = \frac{6~m}{tan(24,78^\circ)}$
${x} \approx {13~m}$
Der Abstand zwischen der Oma und dem Punkt auf dem Boden unter dem Ballon beträgt also ungefähr $13$ Meter.
Wenn wir nun diese beiden Längen voneinander subtrahieren, erhalten wir die Entfernung zwischen dem Mädchen und seiner Oma.
$13~m - 7~m = 6~m$
Die Oma und das Mädchen stehen $6$ Meter voneinander entfernt.
Du hättest die Aufgabe im Übrigen auch anders lösen können. Häufig gibt es mehrere Möglichkeiten. Wichtig ist, dass du am Ende auf das richtige Ergebnis kommst.
Nun hast du einen Überblick darüber bekommen, wie man mit den Winkelfunktionen rechnet. Um dein Wissen zu vertiefen, teste dich in unseren Aufgaben zur Winkelfunktion mit Sinus, Kosinus und Tangens. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Wir betrachten einen Fernseher, dessen Bildschirm 40 cm hoch und 120 cm breit ist. Ein Elektriker möchte nun wissen, wie lang die Diagonale des Fernsehers ist. Kannst du ihm helfen?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
