Erster und zweiter Strahlensatz: Formel und Erklärung
Die Strahlensätze sind ein wichtiges Thema in der Mathematik. Mit Hilfe der Strahlensätze kannst du zum Beispiel die Breite eines Flusses, die Höhe eines Turmes, eines Hauses oder eines Berges berechnen. Um mit den Strahlensätzen rechnen zu können, musst du jedoch erst einmal die Voraussetzungen für die Strahlensätze kennen lernen.
Strahlensätze - Erklärung
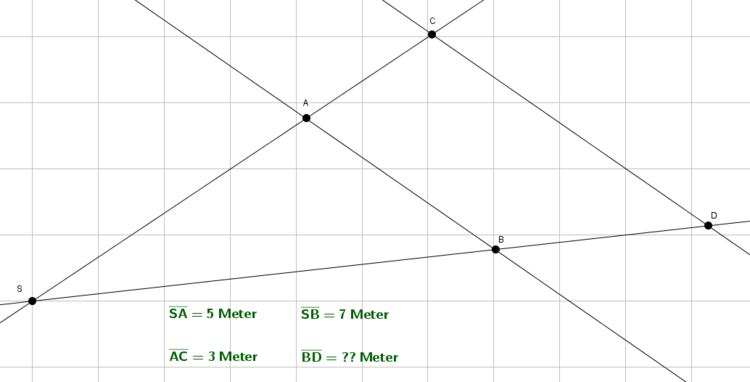
Strahlensätze können nur angewandt werden, wenn zwei (oder mehrere) Strahlen den gleichen Anfangspunkt besitzen. Zudem müssen diese Strahlen von zwei Geraden oder auch Strecken gekreuzt werden. Diese zwei Geraden bzw. Strecken müssen parallel zueinander sein. Es ist dabei egal, ob die parallelen Geraden/Strecken beide rechts bzw. links vom Anfangspunkt der Strahlen liegen oder ob sie auf unterschiedlichen Seiten des Anfangspunktes liegen. (Gucke dir dazu die beiden Abbildungen an, dann verstehst du, was wir meinen.)
Gut zu wissen
Strecken sind Verbindungslinien zwischen zwei Punkten, haben also einen Anfangspunkt und einen Endpunkt. Geraden sind endlos lang, besitzen also weder einen Anfangspunkt noch einen Endpunkt. Gerade können aber durch Punkte verlaufen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
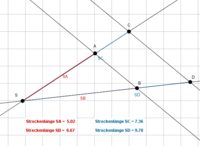
1. Strahlensatz
Im Bild wird der 1. Strahlensatz gezeigt. Der 1. Strahlensatz setzt ein Verhältnis aus zwei Teilabschnitten des einen Strahles gleich mit dem Verhältnis aus den entsprechenden Teilabschnitten des anderen Strahles. Somit stehen auf der einen Seite der Gleichung immer Strecken des einen Strahles und auf der anderen Seite der Gleichung die entsprechenden Strecken des anderen Strahles.
In Bezug auf die obige Abbildung gilt nach dem 1. Strahlensatz die Formel:
$\frac{\overline{SA}}{\overline{SC}} =\frac{\overline{SB}}{\overline{SD}}$ bzw.
$\frac{\overline{SA}}{\overline{AC}} =\frac{\overline{SB}}{\overline{BD}}$ bzw.
$\frac{\overline{AC}}{\overline{SC}} =\frac{\overline{BD}}{\overline{SD}}$
Bei jeder Gleichung können Zähler und Nenner auch vertauscht werden. Wenn du jedoch Zähler und Nenner auf der einen Seite der Gleichung vertauscht, musst du dies natürlich auch auf der anderen Seite der Gleichung machen.
Der 1. Strahlensatz vergleicht das Verhältnis der Teilabschnitte des einen Strahles mit dem Verhältnis der Teilabschnitte des anderen Strahles. Die Längen der Parallelen werden nicht beachtet.
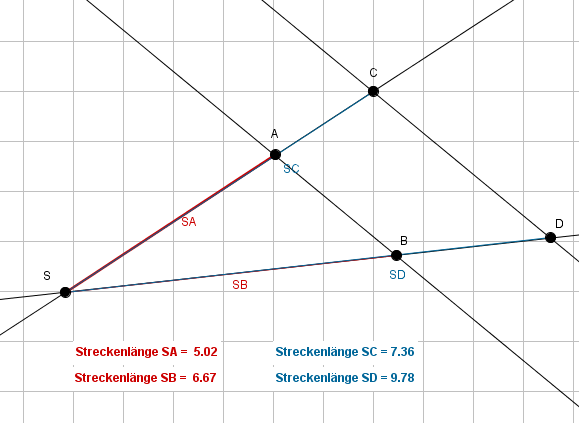
2. Strahlensatz
Der 2. Strahlensatz berücksichtigt nun die Längen der beiden parallelen Strecken. Der 2. Strahlensatz setzt das Verhältnis von zwei Teilabschnitten des einen Strahles gleich mit dem Verhältnis der zwei parallelen Strecken.
In Bezug auf die obige Abbildung gilt nach dem 2. Strahlensatz die Formel:
$\frac{\overline{SA}}{\overline{SC}} =\frac{\overline{AB}}{\overline{CD}}$ bzw.
$\frac{\overline{SB}}{\overline{SD}} =\frac{\overline{AB}}{\overline{CD}}$
Bei jeder Gleichung können Zähler und Nenner auch vertauscht werden. Wenn du jedoch Zähler und Nenner auf der einen Seite der Gleichung vertauscht, musst du dies natürlich auch auf der anderen Seite der Gleichung machen.
Beispiel
Nun noch ein Zahlenbeispiel zum zweiten Strahlensatz:
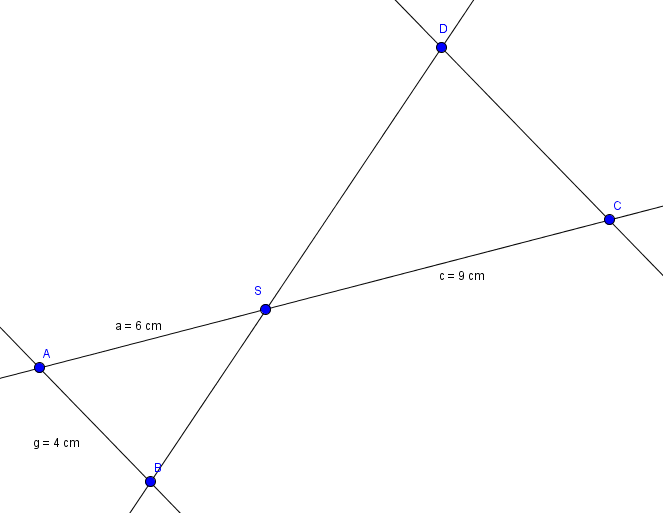
In dem Bild sehen wir zwei Strahlen, die von zwei Parallelen gekreuzt werden. Bekannt sind die Längen der Seiten a, c und g. Wir wollen die Länge der Seite $\overline{CD}$ herausfinden. Wir nennen sie zur besseren Verständlichkeit einfach $x$.
Da wir die Länge einer Parallelen finden wollen, können wir den ersten Strahlensatz nicht anwenden. Also müssen wir den 2. Strahlensatz anwenden:
$\frac{a}{c} = \frac{g}{x}$
Auf der einen Seite der Gleichung stehen die Teilabschnitte eines Strahls und auf der anderen Seite der Gleichung die Parallelen. Im Zähler steht auf der linken Seite der Gleichung die Strecke, die bis zum Punkt $A$ führt und daher auf der rechten Seite der Gleichung auch die Parallele, die bis zum Punkt $A$ führt. Im Nenner steht auf der linken Seite der Gleichung die Strecke, die bis zum Punkt $C$ führt und daher auf der rechten Seite der Gleichung auch die Parallele, die bis zum Punkt $C$ führt.
Wir setzen nun die gegebenen Werte ein, und erhalten so:
$\frac{6 \;cm}{9 \;cm} = \frac{4 \;cm}{x}$
Diese Gleichung können wir nach $x$ auflösen und erhalten dann: $x= 6~cm$
Die Strecke $\overline{CD}$ ist also $6~cm$ lang.Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
