Die Winkelfunktionen Sinus, Kosinus und Tangens verwendest du, wenn du die Länge einer Seite oder die Größe eines Winkels in einem rechtwinkligen Dreieck berechnen möchtest.
Zunächst widmen wir uns der Definition des Sinus.
Definition des Sinus
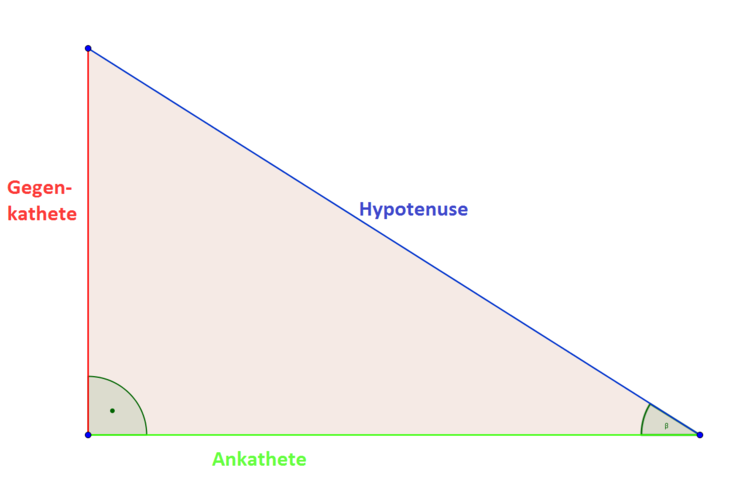
Die erste Winkelfunktion, die wir behandeln, ist der Sinus. Er beschreibt das Verhältnis von Gegenkathete zu Hypotenuse.
Merke
Der Sinus von $\alpha$ (geschrieben $\sin( \alpha)$) ist die Gegenkathete von $\alpha$ geteilt durch die Hypotenuse. Somit beschreibt $\sin( \alpha)$ das Verhältnis der Längen von Gegenkathete und Hypotenuse. Das mag zunächst ein wenig kompliziert klingen, aber die folgenden Beispiele zeigen dir, dass es eigentlich ganz einfach ist.
Was können wir mit dem Sinus berechnen?
Mit dem Sinus kann man entweder die Länge der Hypotenuse oder die Länge der Gegenkathete oder die Größe des Winkels berechnen, je nachdem, welche der drei Größen gesucht ist. Die jeweils anderen beiden Größen müssen gegeben sein.
Methode
$Winkel = sin^{-1}(\frac{Gegenkathete}{Hypotenuse})$
$Gegenkathete = sin(Winkel)\cdot Hypotenuse$
$Hypotenuse = \frac{Gegenkathete}{sin(Winkel)}$
Auf diese Formeln kommst du durch Umformung der Grundformel $sinus (\alpha) = \frac{Gegenkathete}{Hypotenuse}$. Daher musst du diese Formeln nicht auswendig lernen. Es ist aber dennoch hilfreich sie zu kennen. Vor allem, da du Aufgaben schneller lösen kannst, wenn du nicht erst die Formel umstellen musst.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Sinus - Aufgaben mit Lösungen
Beispiel
Winkel
Um die Größe des Winkels $\alpha$ zu berechnen, musst du zuerst das Verhältnis von Gegenkathete zu Hypotenuse bestimmen. Also einfach $\frac{Gegenkathete}{Hypotenuse}$ ausrechnen. Das Ergebnis davon wird dann in die Umkehrfunktion von Sinus, also in $sin ^{-1}$, eingesetzt.
Beispiel
$\alpha =~?$, Hypotenuse $=~6~cm$, Gegenkathete $=~3~cm$
$sin(\alpha) = \frac{Gegenkathete}{Hypotenuse}$
$sin(\alpha) = \frac{3~cm}{6~cm} = {0,5}$
$\alpha = {sin^{-1}(0,5)} = 30 ^\circ$
Somit gilt: $\alpha$ = $30^\circ$
Beispiel
Gegenkathete
Zur Berechnung der Gegenkathete benötigst du die Länge der Hypotenuse und die Größe des Winkels. Du setzt beide Werte in die Formel ein und stellst die Formel dann nach der Gegenkathete um.
Beispiel
$\alpha = 30 ^\circ$ , Hypotenuse = $8,5~cm$ , Gegenkathete = $?$
$sin(\alpha) = \frac{Gegenkathete}{Hypotenuse}$
$sin(30 ^\circ) = \frac{Gegenkathete}{8,5~cm}$
$sin(30 ^\circ)\cdot 8,5~cm = {Gegenkathete}$
$Gegenkathete = 4,25~cm$
Die Gegenkathete ist 4,25 cm lang.
Übrigens haben die Ergebnisse meist viele Nachkommastellen. Also wundere dich nicht, wenn dein Ergebnis viele Nachkommastellen hat. Du kannst das Ergebnis dann auf zwei Nachkommastellen runden.
Beispiel
Hypotenuse
Zuletzt zur Berechnung der Hypotenuse. Hierfür brauchst du die Länge der Gegenkathete und die Größe des Winkels.
Du setzt beide Werte wieder in die Formel ein. Dann stellst du die Formel nach der Hypotenuse um.
Beispiel
$\alpha = 45 ^\circ $ , Hypotenuse $=~?~cm$ , Gegenkathete $=~4~cm$
$sin(\alpha) = \frac{Gegenkathete}{Hypotenuse}$
$sin(45 ^\circ) = \frac{4~cm}{Hypotenuse}$
$sin(45 ^\circ)\cdot Hypotenuse = {4~cm}$
$ Hypotenuse = \frac{4~cm}{sin(45 ^\circ)}$
$ Hypotenuse = 4\sqrt{2}~cm {\approx} 5,657~cm$
Somit ist die Hypotenuse ungefähr 5,657 cm lang.
Merke
In manchen Aufgaben sind die Seiten in unterschiedlichen Längeneinheiten angegeben. Dies kann vorkommen, wenn die Größe des Winkels gesucht ist und die Lägen der Gegenkathete und der Hypotenuse gegeben sind. Bevor du die Werte der Seiten in die Formel einsetzt, musst du die Längen dann zunächst so umrechnen, dass sie in derselben Einheit stehen, beispielsweise beide Seiten in Zentimeter oder beide Seiten in Meter.
Jetzt weißt du, wie man mit der Winkelfunktion Sinus umgeht. Dein neues Wissen kannst du nun an unseren Übungsaufgaben testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Übungsaufgaben
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Weitere Erklärungen & Übungen zum Thema
Mathematik
> Geometrie
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
