Kosinus - Rechnen mit der Winkelfunktion
Sinus, Kosinus und Tangens kommen insbesondere in der Geometrie für Berechnungen an Dreiecken vor - sie begegnen dir aber auch in der Analysis.
Zunächst widmen wir uns der Definition des Kosinus.
Definition des Kosinus
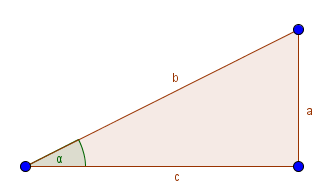
Der Kosinus ist die zweite Winkelfunktion, die wir behandeln. Er gibt das Verhältnis zwischen Winkel, Ankathete und Hypotenuse an. Der Kosinus wird mathematisch $\cos(\alpha)$ abgekürzt.
Merke
$cos(\alpha) = \frac{Ankathete}{Hypotenuse}$
Mit dem Kosinus kannst du rechnen, wenn du zwei der drei Größen, Winkel, Ankathete und Hypotenuse gegeben hast und die dritte suchst. Das Vorgehen ist also ähnlich wie beim Sinus, nur mit der Ankathete anstatt der Gegenkathete eines Winkels.
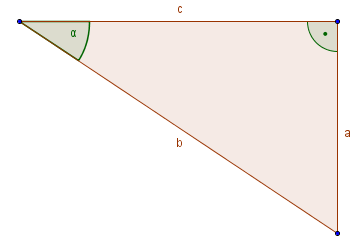
$cos (\alpha) = \frac{Ankathete}{Hypotenuse}$
Auf das obere Bild bezogen, ergibt sich aus der Formel: $cos(\alpha) = \frac{c}{b}$
Methode
$Winkel = cos^{-1}(\frac{Ankathete}{Hypotenuse})$
$Ankathete = cos(Winkel)\cdot Hypotenuse$
$Hypotenuse = \frac{Ankathete}{cos(Winkel)}$
Auf diese Formeln kommst du durch Umformung der Grundformel $cos (\alpha)= \frac{Ankathete}{Hypotenuse}$. Daher musst du diese Formeln nicht auswendig lernen. Es ist aber dennoch hilfreich sie zu kennen. Vor allem, da du Aufgaben schneller lösen kannst, wenn du nicht erst die Formel umstellen musst.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele zum Rechnen mit dem Kosinus
Beispiel
Winkel
Berechnung des Winkels $\alpha$ mit dem Kosinus.
$\alpha = ?$, Ankathete= $10~cm$, Hypotenuse =$ 2~dm$
$cos(\alpha) = \frac{Ankathete}{Hypotenuse}$
$cos(\alpha) = \frac{10cm}{2dm} = \frac{10cm}{20cm}$
$\cos ^{-1} (cos (\alpha))= cos^{-1}(\frac{10cm}{20cm})$
$\alpha = cos^{-1}(\frac{10}{20})$
$\alpha = 60^\circ$
$\frac{cm}{cm}$ kürzt sich weg. Wir müssen den $cos^{-1}$ anwenden, da $\alpha$ allein stehen muss.
Somit gilt: $\alpha$ = $60^\circ$
Beispiel
Ankathete
Berechnung der Ankathete (hier c) mit dem Kosinus.
$\alpha = 80 ^\circ$, Ankathete = ?, Hypotenuse = $6,7mm$
$cos(\alpha) = \frac{Ankathete}{Hypotenuse}$
$cos(80^\circ) = \frac{c}{6,7mm}$
${cos(80^\circ)}\cdot{6,7mm} = c$
${c} \approx {1,16~mm}$
Die Ankathete ist also 1,16 mm groß.
Beispiel
Hypotenuse
Berechnung der Hypotenuse (hier b) mit dem Kosinus.
$\alpha = 30^\circ$, Ankathete = $8~cm$, Hypotenuse = ?
$cos(\alpha) = \frac{Ankathete}{Hypotenuse}$
$cos(30^\circ) = \frac{8~cm}{b}$
${cos(30^\circ)}\cdot{b} = 8~cm$
$b = \frac{8~cm}{cos(30^\circ)}$
${b} \approx {9,24~cm}$
Die Hypotenuse ist ca. 9,24 cm lang.
Jetzt weißt du, wie man mit der Winkelfunktion Kosinus umgeht. Dein neues Wissen kannst du nun an unseren Übungsaufgaben testen. Dabei wünschen wir dir viel Spaß und Erfolg!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
