Lineare Funktionen - Definition und Erklärung
Funktionen sind ein wichtiger Bestandteil der Mathematik. Eine Art sind die linearen Funktionen (lineare Zuordnungen), diese Art von Funktionsgleichungen werden wir dir hier im Detail erklären.
Linearen Funktionen: Definition
Eine Funktion stellt immer das Verhältnis zweier Variablen dar. Meist werden die zwei Variablen $x$ und $y$ genannt. Dieses Verhältnis kann dann durch eine Gleichung ausgedrückt und in einem Koordinatensystem eingezeichnet werden.
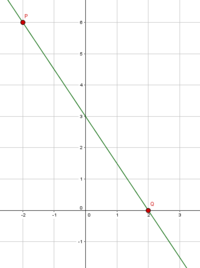
Lineare Funktionen beschreiben immer ein lineares Verhältnis, bzw. eine lineare Zuordnung zwischen zwei Variablen. Daher sind ihre Graphen eine gerade Linie im Koordinatensystem.
Mathematisch ausgedrückt geht es um folgenden Zusammenhang:
Merke
Merke
$f(x) = \textcolor{red}{m}\cdot x + \textcolor{blue}{n}$
$\textcolor{red}{m : Steigung}$
$\textcolor{blue}{n : y-Achsenabschnitt}$
$x :$ unabhängige Variable
$f(x) = y :$ abhängige Variable
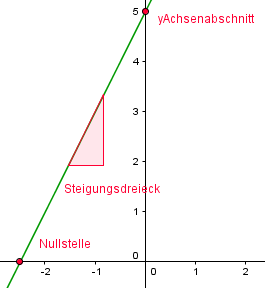
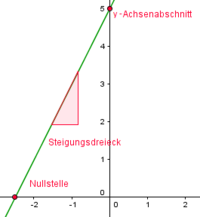
Dabei sind alle Variablen, also $x$ und $y$ ( $y$ ist das Gleiche wie $f(x)$ ), $m$ und $n$, beliebige Zahlen. Je nach Besonderheit der Zahlen, sehen die Funktionen dann etwas anders aus. Es handelt sich jedoch immer um eine gerade Linie!
Schauen wir uns ein Beispiel an.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Lineare Funktionen: Beispielaufgabe
Kosten pro gekaufter Kugel Eis
Wir wollen eine Funktion erstellen, welche das Verhältnis zwischen der Anzahl gekaufter Kugeln Eis zum Preis abbildet.
Nehmen wir an, eine Kugel Eis kostet $0,80$ €. Nun können wir aufgrund dieser Information die Kosten für zwei, drei, vier usw. Kugeln ausrechnen.
| Anzahl der Kugeln | Kosten (in €) |
| 0 | 0 |
| 1 | 0,80 |
| 2 | 1,60 |
| 3 | 2,40 |
| 4 | 3,20 |
| 5 | 4,00 |
| 6 | 4,80 |
| 7 | 5,60 |
Wir haben die Kosten im Verhältnis zur Anzahl der Kugeln in eine Tabelle eingetragen. Somit erhalten wir die dazugehörige Wertetabelle.
Dieses Verhältnis zwischen Kosten und Anzahl können wir nun in einer Funktion abbilden. Da die Kosten proportional ansteigen, erhalten wir eine lineare Funktion.
Zeichne die dazugehörige Funktion zuerst einmal selbst! Du kannst die Werte aus der Tabelle einfach ablesen und in ein passendes Koordinatensystem einzeichnen.
Methode
Methode
In der Wertetabelle stehen die x-Werte links und die dazugehörigen y-Werte rechts. Bei unserem Beispiel ordnen wir die Anzahl der Kugeln den Kosten zu. Somit muss die Anzahl der Kugeln dem $x-Wert$ entsprechen, denen ein $y$, der Preis, zugeordnet wird.
In einem Koordinatensystem verläuft immer von links nach rechts die $x-Achse$ und von unten nach oben die $y-Achse$.
Wir nehmen nun z.B. den Punkt $(2/1,6)$ und suchen zuerst die $2$ auf der x-Achse und ziehen gedanklich eine Linie nach oben und dann die $1,6$ auf der y-Achse und ziehen wieder eine gedanklich Linie nach rechts. Da wo sich die beiden "Gedankenlinien" treffen setzten wir den Punkt.
$P (x-Wert / y-Wert)$
Dies machen wir nun mit mehreren Punkten, verbinden diese und erhalten eine Funktion.
So sollte die Funktion aussehen:
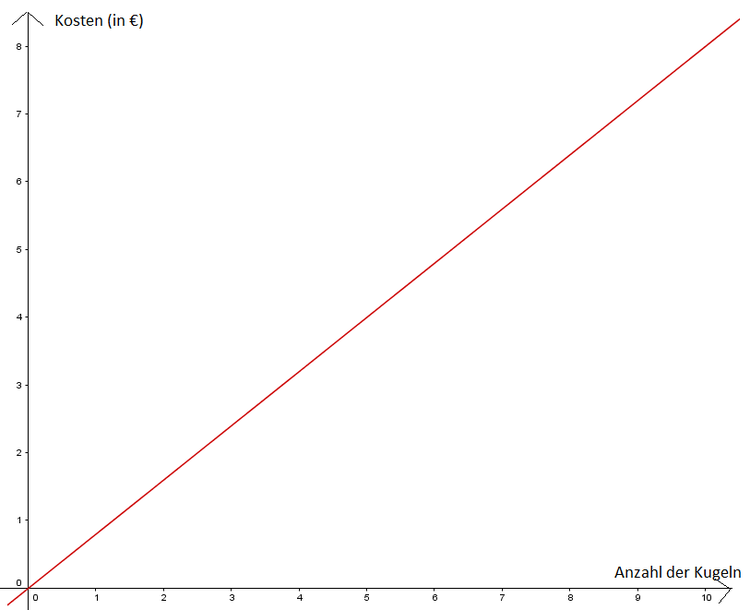
Auf der $x$-Achse ist die Anzahl der Kugeln abgebildet und auf der $y$-Achse die Kosten. Die Funktion bildet das Verhältnis dazwischen ab.
Wir können sehen, dass die Funktion die Punkte der Wertetabelle miteinander verbindet und eine gerade Linie entsteht.
Lineare Funktionen: Besonderheiten der Variablen
$n$: Der y-Achsenabschnitt - der Schnittpunkt mit der y-Achse - liegt bei null, da keine Kugel Eis auch nichts kostet.
Allgemein zeigt der y-Achsenabschnitt das Verhältnis zwischen keinem $x$ und $y$.
$m$: Die Steigung ist positiv - je größer die $x$-Werte werden, desto größer werden die $y$-Werte. Natürlich, denn je mehr Kugeln gekauft werden, umso teurer wird es.
Die Steigung kann auch negativ sein. Dann ist $m$ ein negativer Wert.
$x$ und $y$: Die zwei Variablen sind hierbei die Anzahl der Kugeln und der Preis. Beide Variablen stehen im Verhältnis zueinander. Dabei ist $x$ die unabhängige Variabel, auch Funktionsargument genannt, und $y$ die abhängige Variable.
Lineare Funktionsgleichung bestimmen
Wir können die Funktionsgleichung, die das Verhältnis zwischen Kugeln Eis und Preis wiedergibt, bestimmen.
Dies hat den Vorteil, dass man sowohl für jede beliebe Anzahl an Kugeln den Preis ausrechnen kann, als auch für jeden beliebigen Preis die Anzahl der Kugeln ermitteln kann.
Dafür nehmen wir uns zwei beliebige Punkte, zum Beispiel $P(0/0)$ und $Q(1/0,8)$. Die Punkte setzen wir jetzt nacheinander in die "leere" lineare Gleichung $f(x) = m\cdot x +n$ ein.
1. $P(0/0)$
Dieser Punkt besagt, dass der y-Achsenabschnitt, also $n$, gleich null ist. Wie oben schon erwähnt, ist der Preis für keine Kugel auch $0 €$.
Mathematisch können wir den Punkt einfach einsetzen. Dann erhalten wir die Gleichung:
$0 = m \cdot 0 + n$
$0 = n$
Also fällt das $n$ aus der Gleichung weg.
2. $Q(1/0,8)$
Nun zum zweiten Punkt $Q(1/0,8)$. Sachlich gesehen hat dieser Punkt die Bedeutung, dass eine Kugel $0,80 €$ kostet. Daher muss die Steigung $0,8$ betragen.
Schauen wir uns dies mathematisch an, indem wir den Punkt in die Gleichung einsetzen.
$y = m \cdot x$
$0,8 = m \cdot 1$
$0,8 = m$
Somit haben wir nun auch mathematisch gezeigt, dass die Steigung $0,8$ beträgt.
Nun müssen wir die zwei errechneten Variablen noch in unsere Gleichung einsetzen.
Daraus folgt, dass unsere lineare Funktionsgleichung $f(x) = 0,8 \cdot x$ ist.
Nun kennst du die Definition und Anwendung linearer Funktionen und Funktionsgleichungen. Ob du diese Erklärungen verstanden hast, kannst du mit den Übungsaufgaben überprüfen. Viel Spaß dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
