Lineare Funktion bestimmen mithilfe eines Steigungsdreiecks
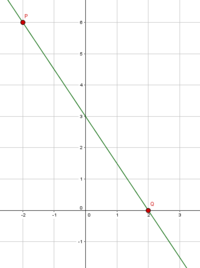
Wie kann man aus einem abgebildeten Graphen einer linearen Funktion die dazugehörige Funktionsgleichung bestimmen? Eine einfache Methode ist es, den y-Achsenabschnitt abzulesen und die Steigung mit Hilfe eines Steigungsdreiecks zu bestimmen. In diesem Lerntext werden wir die Steigung einer Funktion unter Zuhilfenahme eines Steigungsdreiecks bestimmen.
Gleichung einer linearen Funktion bestimmen
Der Graph einer linearen Funktion ist immer eine Gerade. Daher ist die Steigung in jedem Punkt des Graphen gleich. Um die Gleichung zu bestimmen zeichnet man ein Steigungsdreieck, um die Steigung $m$ zu bestimmen. Den y-Achsenabschnitt $n$ liest man dann im nächsten Schritt von der Abbildung ab. Nachdem man beide Variablen bestimmt hat, setzt man diese in die allgemeine Form ein und erhält die Funktionsgleichung.
Merke
Merke
allgemeine Form
$f(x) = \textcolor{red}{m}\cdot x + \textcolor{blue}{n}$
$\textcolor{red}{m : Steigung}$
$\textcolor{blue}{n : y-Achsenabschnitt}$
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
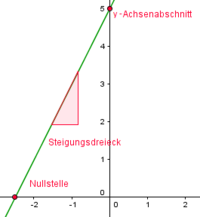
Steigungsdreieck einzeichnen und berechnen
Methode
Methode
Vorgehensweise
1. Zwei beliebige Punkte auf dem Graphen aussuchen.
2. Punkte durch ein Dreieck verbinden.
3. Den Höhen- und Längenunterschied ermitteln.
4. Die Steigung berechnen.
$\rightarrow Steigung = \frac{\textcolor{orange}{Höhenunterschied}}{\textcolor{blue}{Längenunterschied}} = \frac{\textcolor{orange}{y_2 - y_1}}{\textcolor{blue}{x_2 - x_1}} $
Mit einem Steigungsdreieck können wir die Steigung jeder linearen Funktion ganz leicht bestimmen. Dafür müssen wir zwei Punkte auf der Geraden aussuchen.
1. Zwei beliebige Punkte aussuchen:
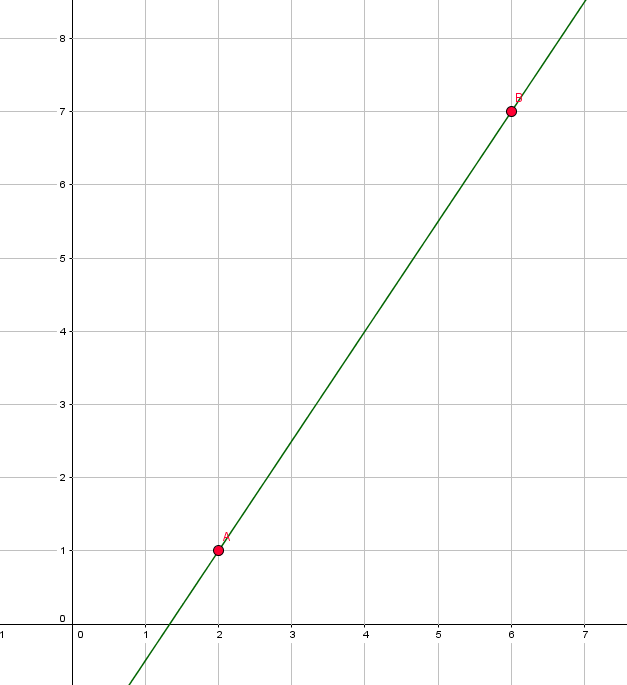
Wir wählen zwei beliebige Punkte auf der Funktion aus. Am besten suchen wir Punkte mit ganzen Zahlen, damit keine Ablesefehler entstehen.
2. Die Punkte durch ein Dreieck verbinden:
Mit den zwei Punkten und dem Graphen wird ein Dreieck gebildet. Dabei entsteht ein Hilfspunkt (hier $C$), an dem ein rechter Winkel sein muss.
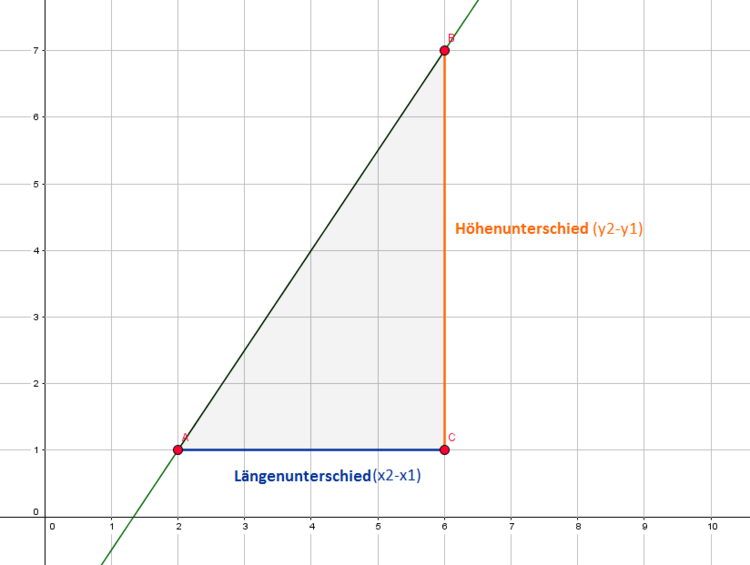
Nun haben wir unser Steigungsdreieck eingezeichnet und können den Höhen- und Längenunterschied ablesen.
3. Höhen- und Längenunterschied bestimmen:
Für den Längenunterschied muss die Differenz zwischen den beiden x-Werten errechnet werden. Um den Höhenunterschied zu ermitteln gehen wir genauso bei den y-Werten vor. Wir ziehen jeweils die Werte voneinander ab. Hier sind die Punkte $\textcolor{red}{A}$ und $\textcolor{blue}{B}$ gegeben. Wenn der Höhenunterschied mit $y_\textcolor{red}{A}-y_\textcolor{blue}{B}$ berechnet wird, dann muss der Längenunterschied mit $x_\textcolor{red}{A}-x_\textcolor{blue}{B}$ berechnet werden. $A$ und $B$ dürfen hier nicht vertauscht werden, da sonst ein Vorzeichenfehler entsteht.
Die Werte können wir einfach aus dem Koordinatensystem ablesen.
4. Steigung berechnen:
Um nun aus dem Höhen- und Längenunterschied die Steigung zu ermitteln, müssen wir diese teilen.
Merke
Merke
$Steigung = \frac{\textcolor{orange}{Höhenunterschied}}{\textcolor{blue}{Längenunterschied}} = \frac{\textcolor{orange}{y_2 - y_1}}{\textcolor{blue}{x_2 - x_1}} $
Welche Steigung hat die oben abgebildete Funktion dann?
Vertiefung
Lösung
Längenunterschied: Dafür lesen wir zuerst die beiden $x-Werte$ ab. Der größere liegt bei Punkt $B$ und beträgt $6$, der kleinere bei Punkt $A$ und hat den Wert $2$. Nun ziehen wir $2$ von $6$ ab und wissen, dass der Längenunterschied $4$ beträgt.
Den Längenunterschied haben wir schon berechnet, dabei haben wir den x-Wert von Punkt $B$ von Punkt $A$ abgezogen. Also ziehen wir den y-Wert von Punkt $B$ von Punkt $A$ ab, um den Höhenunterschied zu bestimmen. $7-1=6$
$Steigung = m = \frac{Höhenunterschied}{Längenunterschied} = \frac{y_2 - y_1}{x_2 - x_1} = \frac {7-1}{6-2} = \frac {6}{4} = \frac {3}{2} = 1,5$
Für das vollständige Bestimmen der Funktionsgleichung ist noch das Ablesen des y-Achsenabschnittes notwendig und das Eintragen beider Werte in die allgemeine Funktionsgleichung.
Mit den Übungsaufgaben kannst du überprüfen, ob du alles richtig verstanden hast. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
Jetzt registrieren und kostenlose Probestunde anfordern.
Dein Gratis-Lernpaket:
- Nachhilfe-Probestunden gratis
- Hausaufgaben-Soforthilfe: 15 Gratis-Minuten
- Lern-Bibliothek: 1 Tag Gratis-Zugang