Schnittpunkt zweier linearer Funktionen berechnen
Wenn wir mehrere Funktionen in ein Koordinatensystem eintragen, können wir feststellen, dass sich diese manchmal in einem Punkt schneiden. Im folgenden Kapitel wollen wir uns den Schnittpunkt von zwei linearen Funktionen anschauen und die Methode, wie du diesen berechnen kannst, erklären.
Zwei sich schneidende Funktionen
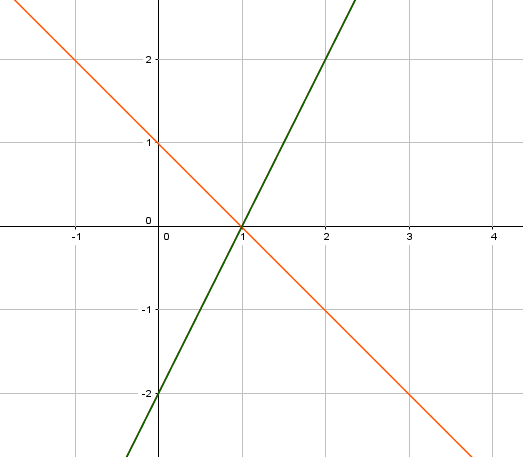
Wenn wir zwei verschiedene Funktionen in ein Koordinatensystem eintragen, dann ist es möglich, dass sich diese schneiden. Wir sehen das in den folgenden Abbildungen:
In der rechten Abbildung können wir den Schnittpunkt direkt ablesen. Er liegt bei $S(1/1)$.
Den Schnittpunkt im linken Bild können wir jedoch durch Ablesen nicht genau bestimmen. Wir müssen ihn daher rechnerisch ermitteln. Zur Berechnung eines Schnittpunktes zweier linearer Funktionen gibt es eine genaue Methode:
Methode
Schnittpunkt zweier linearer Funktionen berechnen
- Funktionsgleichungen gleichsetzen
- x-Wert ermitteln
- y-Wert des Schnittpunkts durch Einsetzen ermitteln
- Probe
Im ersten Schritt der Methode setzen wir die beiden Funktionen gleich. Das machen wir, weil sich die Funktionen den Schnittpunkt teilen, er liegt auf beiden Funktionen. Die x und y-Werte beider Funktionen sind an dieser Stelle also gleich.
Im zweiten Schritt lösen wir dann nach x auf und schreiben alle x-Werte auf eine, alle Zahlenwerte auf die andere Seite des Gleichheitszeichens. Der berechnete x-Wert wird dann in eine der Funktionen eingesetzt, um die y-Koordinate zu erhalten.
Der vierte Schritt ist die Probe, bei der wir die x- und y-Koordinate in beide Funktionen einsetzen und die beiden Werte auf ihre Richtigkeit prüfen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
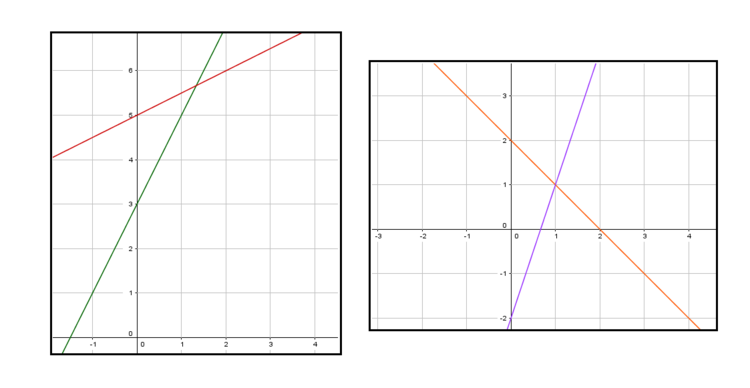
Beispielaufgabe: Schnittpunkt zweier Geraden bestimmen
Die beiden Funktionen $\textcolor{green}{ f(x) = 2\cdot x + 3}$ und $\textcolor{red}{g (x) = 0,5\cdot x + 5}$ sind gegeben und ihr Schnittpunkt soll bestimmt werden.
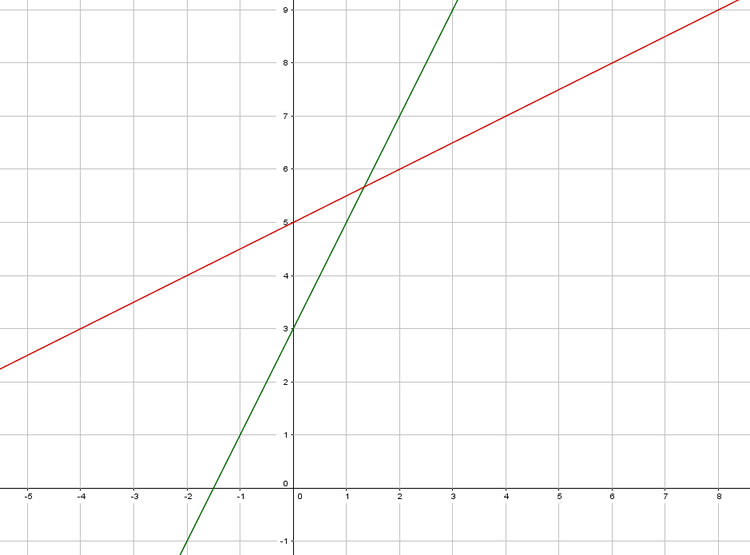
1. Funktionsgleichungen gleichsetzen:
$\textcolor{green}{ f(x) = 2\cdot x + 3}$
$\textcolor{red}{ g(x) = 0,5\cdot x + 5}$
$ \textcolor{green}{2\cdot x + 3} = \textcolor{red}{0,5\cdot x + 5}$
Wir setzen die beiden Gleichungen gleich, da wir den Punkt herausfinden möchten, den beide Funktionen miteinander gemeinsam haben.
2. X-Wert ermitteln:
Wir rechnen mit den gleichgesetzten Gleichungen weiter und formen die Gleichung so um, dass $x$ nur auf einer Seite steht.
$ 2\cdot x + 3 = 0,5\cdot x + 5$ $|-0,5\cdot x$
$ 2\cdot x -0,5\cdot x + 3 = 0,5\cdot x-0,5\cdot x + 5$
$ 1,5\cdot x + 3 = 5$
Alle x-Werte stehen jetzt auf der linken Seite des Gleichheitszeichens. Die Zahlenwerte auf der linken Seite müssen jetzt noch auf die rechte Seite des Gleichheitszeichens gebracht werden. Es ergibt sich:
$ 1,5\cdot x + 3 = 5$ $|-3$
$ 1,5\cdot x = 2$
Da wir aber nicht 1,5 von $x$ suchen, sondern nur ein $x$, müssen wir die Gleichung noch durch $1,5$ teilen, um auf den gesuchten x-Wert zu kommen:
$ 1,5\cdot x = 2$ $|:1,5$
$x = \frac {2}{1,5} = \frac {4}{3} \approx 1,33$
3. Y-Wert des Schnittpunkts durch Einsetzen ermitteln:
Den x-Wert des Schnittpunkts haben wir schon berechnet. Um den dazugehörigen y-Wert auszurechnen, müssen wir den x-Wert einfach in eine der beiden Funktionsgleichungen einsetzen:
$\textcolor{green}{ f(x) = 2\cdot x + 3} $
$f(\frac{4}{3}) = 2\cdot \frac {4}{3} + 3 = \frac {17}{3}$
$\rightarrow S(\frac{4}{3}/\frac{17}{3})$
Wichtig ist dabei, dass wir mit den genauen Zahlen, also den Brüchen rechnen, um Rundungsfehler zu vermeiden.
4. Probe:
Wir können ganz leicht überprüfen, ob wir uns an einer Stelle verrechnet haben.
Dafür setzen wir den x-Wert in die andere Gleichung ein und überprüfen, ob wir den gleichen y-Wert erhalten.
$\textcolor{red}{ g (x) = 0,5\cdot x + 5}$
$g (\frac{4}{3}) = 0,5 \cdot \frac{4}{3} + 5 = \frac{17}{3} \approx 5,67$
Mit den Übungsaufgaben kannst du überprüfen, ob du die Vorgehensweise richtig verstanden hast. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
