Lineare Funktion bestimmen mithilfe von zwei Punkten
Vorgehensweise zum Bestimmen einer linearen Funktionsgleichung mit zwei Punkten
In diesem Lerntext erklären wir dir, wie du aus zwei Punkten eine lineare Funktionsgleichung bestimmst.
Gut zu wissen
Vorgehensweise
1. Die zwei gegebenen Punkte in die allgemeine Form einsetzen.
2. Die beiden Gleichungen untereinanderschreiben.
3. Das Gleichungssystem lösen, sodass wir den Wert der ersten Variable erhalten.
4. Den Wert der Variable in eine der zwei Gleichungen einsetzen und ausrechnen.
5. Den y-Achsenabschnitt und die Steigung in die allgemeine Form einsetzen. $\rightarrow$ Wir erhalten die gefragte Funktionsgleichung.
6. Mache eine Probe!
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispielaufgabe zum Bestimmen einer linearen Funktionsgleichung mit zwei Punkten
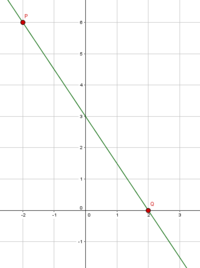
Wir haben die Punkte $P$ und $Q$ gegeben: $P(-2/6)$ $Q(2/0)$.
Um mit ihnen die Funktionsgleichung zu bestimmen, setzen wir die beiden Punkte jeweils in die allgemeine Form $f(x) = m \cdot x +n$ ein.
1. Die Punkte in die allgemeine Form einsetzen:
$P(-2/6)$
$f(-2) = y = m \cdot (-2) +n = 6$
$Q(2/0)$
$f(2) = y = m \cdot 2 +n = 0$
2. Die beiden Gleichungen untereinander schreiben:
$ (-2)\cdot m +n = 6$
$~~~~~~ 2\cdot m +n = 0$
Wir suchen die beiden Variablen $n$ und $m$ und haben zwei Gleichungen gegeben. Daraus folgt, dass wir beide Variablen bestimmen können.
Um das Gleichungssystem zu lösen, müssen wir die beiden Gleichungen miteinander verrechnen. Wenn du dir nicht mehr sicher bist, wie Gleichungssysteme gelöst werden, schaue noch einmal nach, wie man Gleichungssysteme löst.
3. Das Gleichungssystem lösen.
Das Ziel beim Lösen der Gleichungssysteme sollte sein, dass eine der beiden Variablen wegfällt und so nur noch eine übrig bleibt. Diese können wir dann bestimmen. Wir verwenden bei unserem Beispiel das Additionsverfahren zum Lösen von Gleichungssystemen.
$ ~~~~-2\cdot m +n = 6$
$+~~~~~~2\cdot m +n = 0$
$\overline{~~~~~~~~~~~~~~~~~~2\cdot n=6~}$
Wir erhalten eine Gleichung mit einer Variablen, hier $n$. Dies kann nun gelöst werden.
$2\cdot n=6$ $|:2$
$\textcolor{blue}{n = 3}$
Wir haben den Wert für den y-Achsenabschnitt $n$ berechnet.
4. Den Wert der Variable in eine der beiden Gleichungen einsetzen:
Wie können wir die Steigung berechnen? Dafür muss $\textcolor{blue}{n = 3}\;$ in eine der beiden Gleichungen eingesetzt werden. Wir verwenden hier die zweite Gleichung:
$ 2\cdot m +\textcolor{blue}{n} = 0$
$ 2\cdot m + \textcolor{blue}{3}= 0$ $|-3$
$2\cdot m = 0-3$ $|:2$
$m = \frac{- 3}{2} $
$\textcolor{green}{m=- 1,5}$
Also beträgt die Steigung $- 1,5$.
5. Die beiden Variablen in die allgemeine Form einsetzen:
Wir haben beide Variablen $m$ und $n$ ermittelt und müssen diese jetzt nur noch in die allgemeine Form einsetzen, um die Gleichung zu erhalten, die durch beide Punkte verläuft:
$f(x) = m \cdot x +n$
$f(x) = \textcolor{green}{- 1,5} \cdot x + \textcolor{blue}{3}$
6. Probe:
Es ist nicht immer erforderlich eine Probe zu machen, jedoch gibt sie dir die Sicherheit, dass die von dir errechneten Werte der Richtigkeit entsprechen. Um eine Probe durchzuführen gibt es verschiedene Wege. In der folgenden Methode zeichnest du eine Abbildung der Gleichung mithilfe der beiden gegebenen Punkte. Aus dem entstehenden Funktionsgraphen kannst du dann die Steigung und den y-Achsenabschnitt ablesen, welche beide den ermittelten Werten aus deiner Rechnung entsprechen sollten.
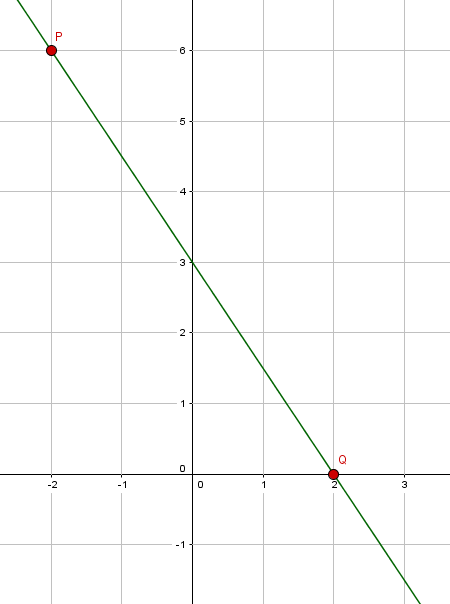
Die beiden Punkte $P$ und $Q$ wurden im Koordinatensystem eingetragen und durch eine Gerade verbunden.
Der Graph der Funktion schneidet die y-Achse im Punkt $R(0/3)$. $\rightarrow n=3$
Auch die Steigung können wir überprüfen. Wenn wir eine Einheit in x-Richtung nach rechts gehen, müssen wir 1,5 Einheiten nach unten. $ \rightarrow m=-1,5$
Überprüfe mit den Übungsaufgaben, ob du eine Funktionsgleichung aus zwei Punkten bestimmen kannst. Viel Erfolg dabei!
Diese Lernseite ist Teil eines interaktiven Online-Kurses zum Thema Mathematik. Das Mathematik-Team erklärt dir alles Wichtige zu deinem Mathematik-Unterricht!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
