Dimensionen der Geometrie: Volumen berechnen
Die Geometrie ist eine der größten Bereiche in der Mathematik. Sie befasst sich mit allen Figuren und Körpern, sei es ein Rechteck, ein Dreieck oder auch andere Figuren. In diesem Kapitel wollen wir einen ersten Einblick in die Geometrie erhalten und betrachten die ersten geometrischen Figuren und eine wichtige Größe, das Volumen.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Volumen
Der Begriff Volumen ist dir vielleicht schon einmal im Alltag begegnet, etwa in der Werbung, wenn es heißt, dass das "Haarshampoo mehr Volumen" verspricht. Doch was hat es mit dem Volumen auf sich?
Das Volumen ist eine geometrische Größe. Es bestimmt, wie viel Raum in einer bestimmten Figur ist. Wenn du beispielsweise eine Badewanne zu Hause hast, dann passt in diese Badewanne eine bestimmte Menge Wasser, bevor diese überläuft. Diese Menge an Wasser, die in die Badewanne passt, nennt man Volumen oder auch Rauminhalt.
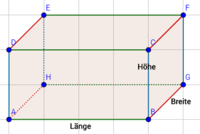
Um das Volumen einer Figur zu bestimmen, benötigst du die Maße der drei verschiedenen Seitenlängen. Die drei verschiedenen Seiten werden jeweils einmal miteinander multipliziert. In einer Formel wäre das dann:
$ Volumen \; = \; \textit{Länge} \;\cdot \;\textit{Höhe} \; \cdot \; Breite$
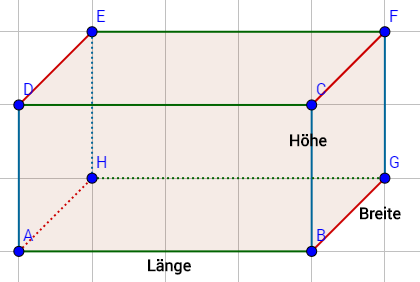
Um also das Volumen einer Figur zu berechnen, benötigst du die drei Seitenlängen. Wichtig ist jedoch auch die Einheit der Längen. Beachte, dass diese übereinstimmen. Falls nicht musst du sie noch umrechnen.
Beispiel Volumen berechnen
Nehmen wir ein Beispiel:
Beispiel
Ein Quader ist gegeben. Dieser hat folgende Werte:
Länge = $10 \; cm$.
Breite = $50 \; mm$.
Höhe = $0,2 \; dm$.
Berechne das Volumen.
Leider kannst du nicht einfach das Volumen des Quaders berechnen, ohne die Werte der Seitenlängen auf eine Einheit zu bringen. Wir bringen also die Seitenlängen auf eine Einheit und erhalten der Reihe nach: Länge: $10 \; cm,$ Breite:$ \; 5 \; cm \;$ und Höhe: $\; 2 \; cm$. Diese Werte multiplizieren wir jetzt noch miteinander und erhalten:
$10 \cdot 5 \cdot 2 \; = \; 50 \cdot 2 \; = \; 100$.
Da du drei Werte miteinander multiplizierst, entsteht auch eine Einheit hoch 3: $cm \cdot cm \cdot cm=$
$100 \; cm^3$.
Wir fassen das Ganze in einer Merkebox zusammen:
Merke
Das Volumen ist eine Größe von dreidimensionalen Figuren.
Das Volumen oder auch der Rauminhalt bestimmt, wie viel in eine Figur hinein passt.
Zur Berechnung des Volumens werden immer drei Werte miteinander multipliziert.
Die Einheit für das Volumen ist immer hoch 3. Man spricht es Kubik aus, etwa Kubikmeter oder Kubikzentimeter.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
