Die Geometrie ist ein großer Bereich in der Mathematik. Sie befasst sich mit allen Figuren und Körpern, sei es ein Rechteck, ein Dreieck oder auch eine Kugel. In diesem Kapitel wollen wir den Einstieg in die Geometrie wagen und schauen uns die ersten geometrischen Figuren und eine wichtige Größe, den Flächeninhalt, an. Dazu erklären wir auch den Begriff Fläche genauer.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Flächeninhalt
Der Flächeninhalt ist eine der ersten Größen in der Geometrie, die du ermitteln sollst. Hierfür werden dir verschiedene geometrische Figuren gegeben, deren Flächeninhalt zu errechnen ist. Doch was genau ist der Flächeninhalt einer Figur?
Jede geometrische Figur hat gewisse Maße, die sie begrenzen. In der nächsten Abbildung siehst du ein Viereck, welches genau $6$ cm lang und $4$ cm hoch ist. Wenn du wissen willst, wie groß die Fläche ist, die diese Figur bedeckt, benötigst du den Flächeninhalt.
Merke
Die Fläche ist der Bereich, den eine Figur einnimmt. Errechnet wird die Fläche über den Flächeninhalt.
Der Flächeninhalt bezeichnet also den Bereich, die eine Figur einnimmt.
Berechnung des Flächeninhaltes
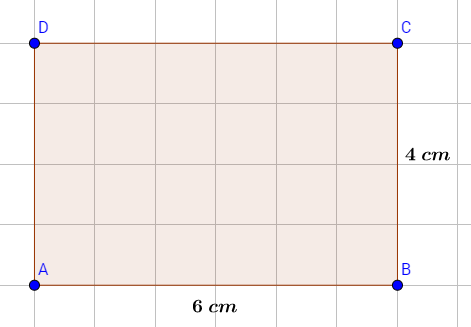
Der Flächeninhalt eines Rechteckes lässt sich durch das Multiplizieren der beiden Seitenlängen ermitteln. In unserem Beispiel ist das also $6 \cdot 4 \;$, was $24$ ergibt. Da wir zwei Werte multiplizieren, muss auch die Einheit multipliziert werden und aus $cm$ wird $cm^2$. Also Lösung für den Flächeninhalt des Beispielrechtecks erhalten wir somit $24cm^2$ und die Aufgabe ist fertig bearbeitet.
Merke
Der Flächeninhalt (A) eines Rechtecks errechnet sich durch die Multiplikation der Grundseite mit der Höhe. Die Höhe muss dabei immer senkrecht auf der Grundseite stehen. Bei einem Parallelogramm ist die Höhe also noch zu ermitteln.
$Flächeninhalt \; = \; Länge\; \cdot \; Höhe$
$A \; = \; g \; \cdot \; h$
Diese Formel gilt für alle regelmäßigen Rechtecke, somit auch für das Parallelogramm und das Quadrat.
Doch die Formel für den Flächeninhalt eines Rechteckes ist nicht dieselbe wie für andere Figuren. So hat beispielsweise das Dreieck eine andere Formel. Dennoch bietet die Formel für den Flächeninhalt des Rechtecks die Basis für den Flächeninhalt weiterer geometrischer Figuren.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen!
Teste dein Wissen!
Übungsaufgaben
Berechne den Flächeninhalt eines Rechtecks mit einer $5\;cm$ Grundseite und einer $2 \; cm $ Höhe.
Wie groß ist die Grundseite, wenn das Rechteck einen Flächeninhalt von $40 \; cm^2$ hat und die Höhe genau $5 \; cm$ lang ist.
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Du möchtest mehr Aufgaben?
Teste kostenlos unser Lernportal mit vielen Übungen & Lösungen.
Du brauchst mehr Hilfe?
Wir unterstützen Dich!
Unsere Kunden über den Studienkreis
Feedback von Eltern & Schüler:innen
Klassenstufen in Mathematik
Weitere Fächer
Lernen und Üben
Noch Fragen?
Wir sind durchgehend für dich erreichbar
