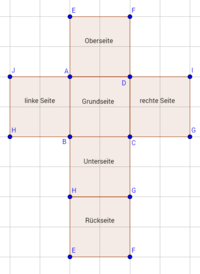
Schrägbilder einfacher Figuren zeichnen
Was sind Schrägbilder?
Schrägbilder sind ein wichtiger Bestandteil der Geometrie. Sie helfen uns, ein Bild von den verschiedensten Figuren zu bekommen, um diese so besser begreifen zu können. In diesem Kapitel bauen wir das Wissen um Schrägbilder aus, indem wir anhand von unterschiedlichen Variablen Schrägbilder erstellen. Hierbei klären wir alle Begrifflichkeiten und geben im Anschluss Übungsaufgaben, um das Thema zu vertiefen.
Methode
Die Grundlage für dieses Kapitel bildet das Wissen über Schrägbilder und Netze. Die Themenseite dazu kannst du durch klicken auf den Begriff erreichen.
In manchen Übungen sollst du mithilfe von Variablen ein Schrägbild einer Figur erstellen. Hierbei ist genau auf die Aufgabenstellung zu achten und darauf, welche Figur erstellt werden soll. Dir sollte etwa bekannt sein, dass ein Würfel immer gleich lange Seiten hat, somit die Höhe und die Länge gleich sind und sich lediglich die Breite durch den Streckungsfaktor, bei der Zeichnung unterscheidet.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiel für die Erstellung von Schrägbildern
Schauen wir uns eine Aufgabe dazu an:
Beispiel
Erstelle ein Schrägbild eines Quaders mit den folgenden Maßen:
Länge = $5 \;cm$, Breite = $4 \;cm$, Höhe = $2\;cm$.
Der erste Schritt sollte das Erkennen der Figur sein. Ein Quader ist ähnlich einem Würfel, jedoch sind nur die gegenüberliegenden Seiten gleich lang.
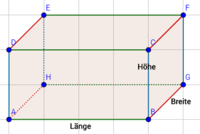
Im nächsten Schritt bestimmen wir, welche Seiten in der Figur die Länge, die Höhe und die Breite bilden:
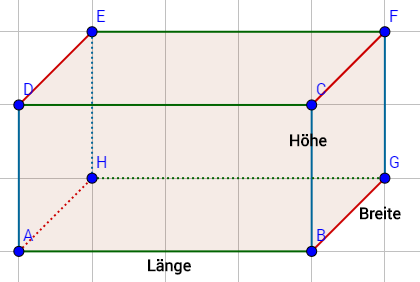
Beginnen wir im nächsten Schritt mit dem Zeichnen. Zuerst kommt die Länge. Diese ist eine gerade Linie, die in unserer Aufgabe exakt $5 \; cm$ lang ist. Wir zeichnen also pro Zentimeter zwei Kästchen im Heft:
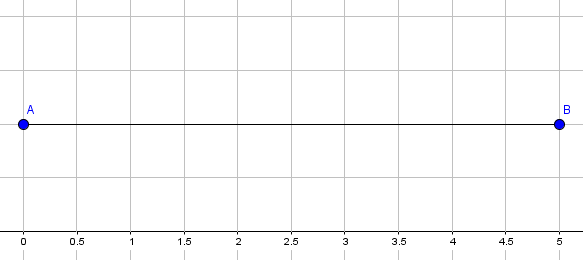
Der nächste Schritt ist die Höhe. Diese liegt genau auf der Länge, jeweils an beiden Punkten:
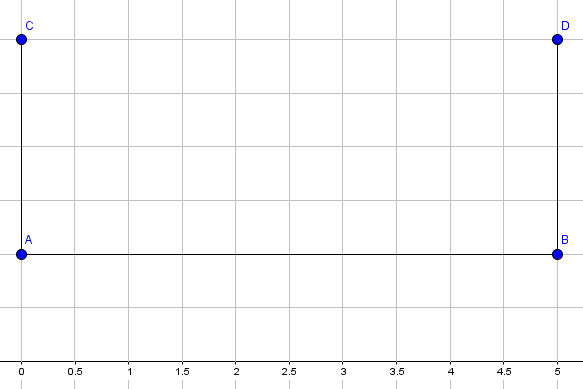
Jetzt können wir auch die beiden Punkte $C$ und $D$ verbinden, sodass die Vorderseite des Schrägbildes entsteht:
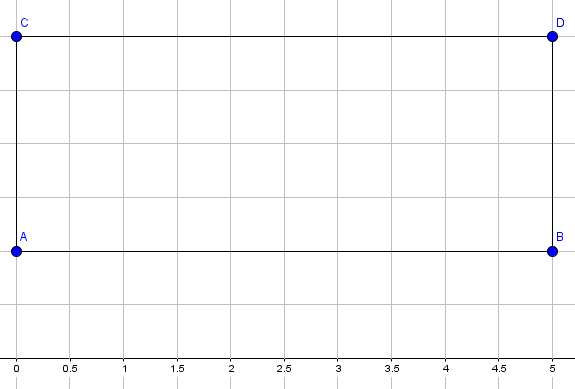
Es fehlt nur noch die Breite, also die Seite, die die Figur dreidimensional aussehen lässt. Diese wird, wie in folgender Abbildung ersichtlich, so eingezeichnet:
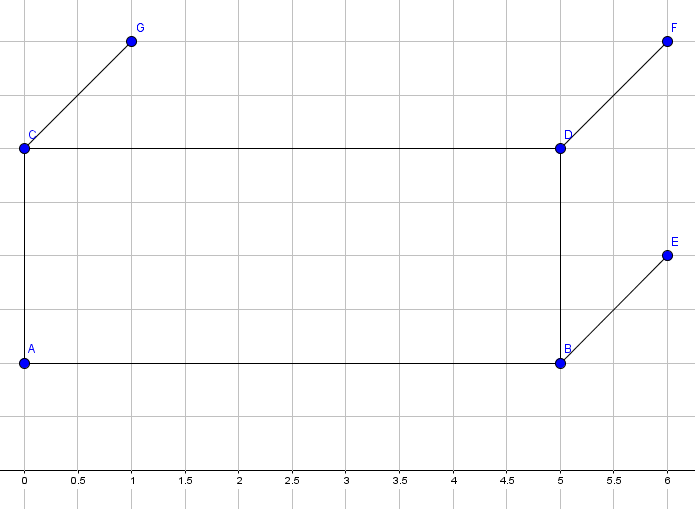
Hierbei werden die Seitenlinien so eingezeichnet, dass sie die Kästchen diagonal durchschneiden. Zudem ist die Länge hier halb so groß, also pro Kästchen wird ein Zentimeter gerechnet. Wir zeichnen von jedem Punkt außerhalb der Figur die Breite ein. Danach verbinden wir die entstandenen Punkte zu einer Figur:
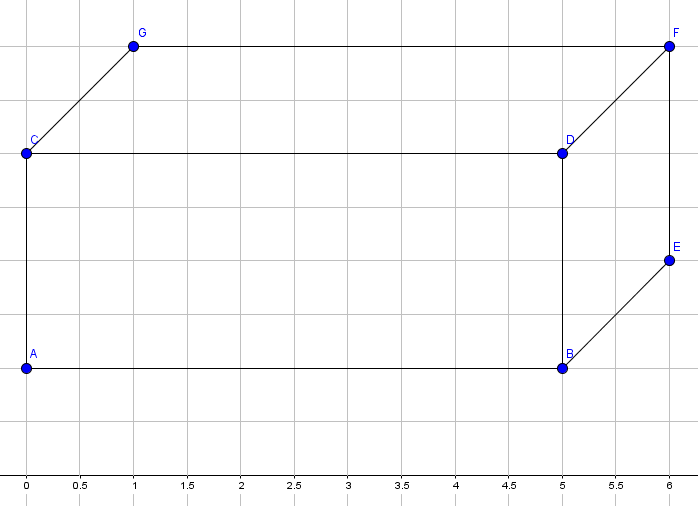
Jetzt fehlt uns nur noch die Hinterseite der Figur, damit es ein richtiger Quader ist. Wir zeichnen auch in der Figur die Breite ein, jedoch gestrichelt und verbinden den neuen Punkt jeweils mit Punkt $G$ und Punkt $E$. Es entsteht die fertige Figur:
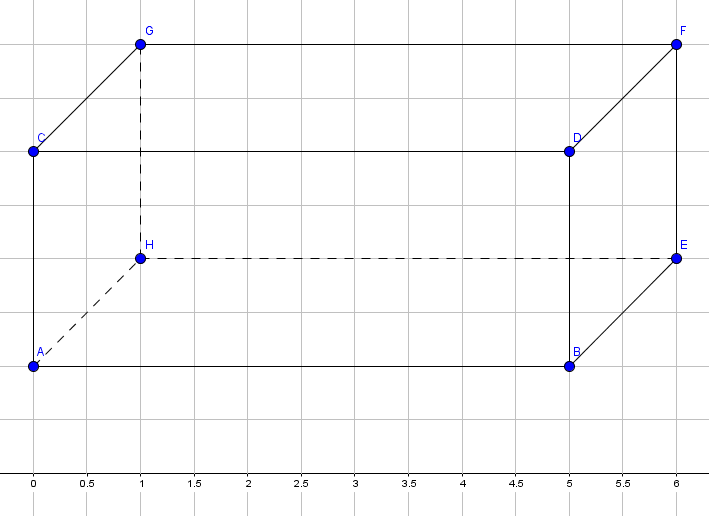
In unserem Beispiel sind wir die Schritte zur Erstellung eines Schrägbildes Schritt für Schritt durchgegangen, in folgender Merkebox sind diese noch einmal zusammengefasst.
Merke
Bei der Erstellung eines Schrägbildes ist die zu zeichnende Figur entscheidend.
Beim Zeichnen beginnen wir bei der Länge, welche mit zwei Kästchen pro Zentimeter eingezeichnet wird.
Nach der Länge folgt die Höhe, auch mit zwei Kästchen pro Zentimeter.
Die Breite ist eine Linie, die die Kästchen diagonal verbindet. Pro Kästchen wir ein Zentimeter gerechnet.
Linien im Hintergrund werden gestrichelt dargestellt.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer