Körpernetze erstellen - Beispiele und Übungsaufgaben
Was sind Schrägbilder und Körpernetze?
Schrägbilder und Körpernetze sind ein Einstiegsthema der Geometrie. Hierbei werden dir verschiedene Figuren in einem Schrägbild gezeigt und du sollst in der Aufgabenstellung das richtige Körpernetz herausfinden. In diesem Kapitel werden wir Figuren auseinandernehmen und schauen, wie sie als Körpernetz aussehen.
Ein Schrägbild ist eine Aufnahme von einem geometrischen Körper aus einer bestimmten Perspektive, beispielsweise von links unten. Hierbei soll das ganze Aussehen der Figur klar werden, es dürfen also keine versteckten Ecken oder Kanten vorhanden sein.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Sofort-Hilfe: Lehrer online fragen
- Gratis Nachhilfe-Probestunde
Beispiele für Schrägbilder und Körpernetze
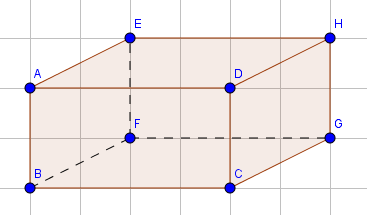
Das erste Schrägbild was wir uns anschauen werden, ist das Schrägbild eines Würfels:
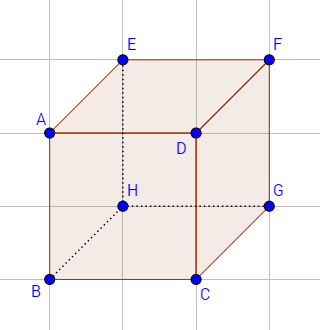
In der Abbildung sehen wir ein Schrägbild eines Würfels. Dieser hat weder versteckte Ecken und Kanten noch irgendeine ausgefallene Form. Diesen wollen wir jetzt in ein Körpernetz bringen. Hierzu schaut man sich im ersten Schritt an, wie viele Flächen die Figur hat. Diese Zahl wird am Ende noch einmal sehr wichtig, wenn wir kontrollieren wollen, ob wir alle Flächen beachtet haben. Bei diesem Würfel haben wir $6$ Flächen.
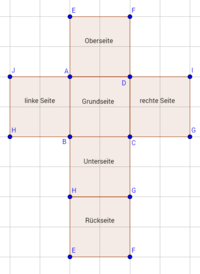
Der zweite Schritt ist das Zerlegen, zuerst im Kopf, dann auf dem Papier: Wir nehmen also eine der Flächen als Grundfläche und legen dann die anderen daneben und dran, sodass beim Zusammensetzen wieder ein Würfel entsteht.
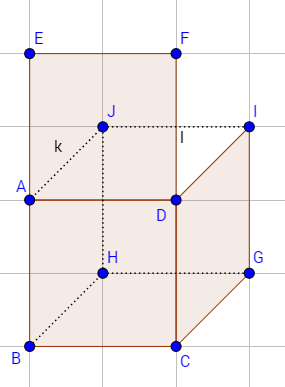
So gehen wir weiter vor, Schritt für Schritt.
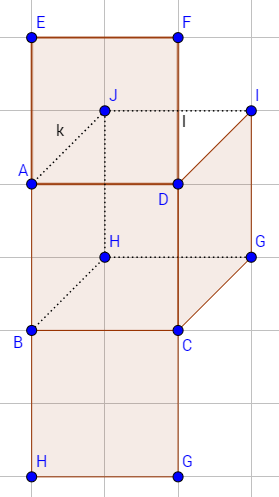
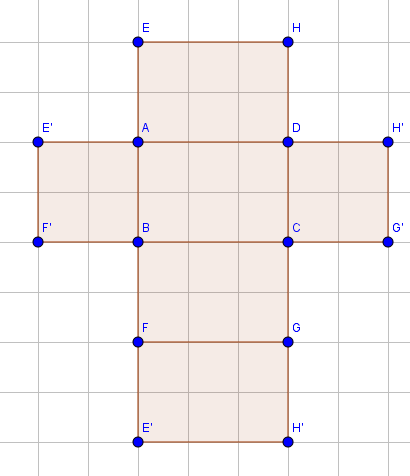
Wir haben jetzt die Oberseite und die Unterseite umgeklappt. Es fehlt also noch die Rückseite, welche wir auch unten an die Unterseite heften, und die jeweilige linke und rechte Seitenfläche, komplett ausgeklappt sieht es dann so aus:
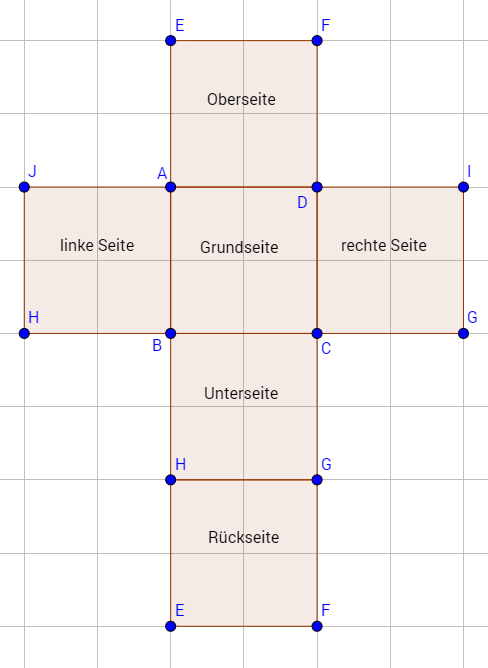
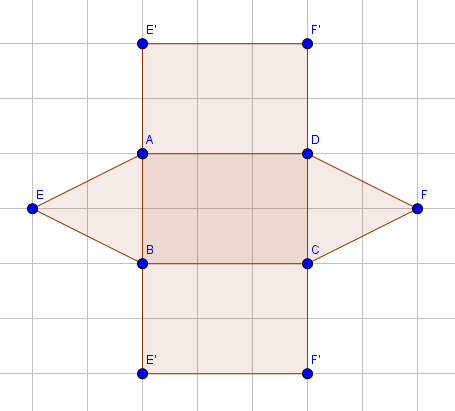
Doch bei der Verwandlung eines Schrägbildes in ein Körpernetz gibt es nicht nur eine richtige Lösung. Der Würfel kann auch anders zerlegt werden und es entsteht diese Figur:
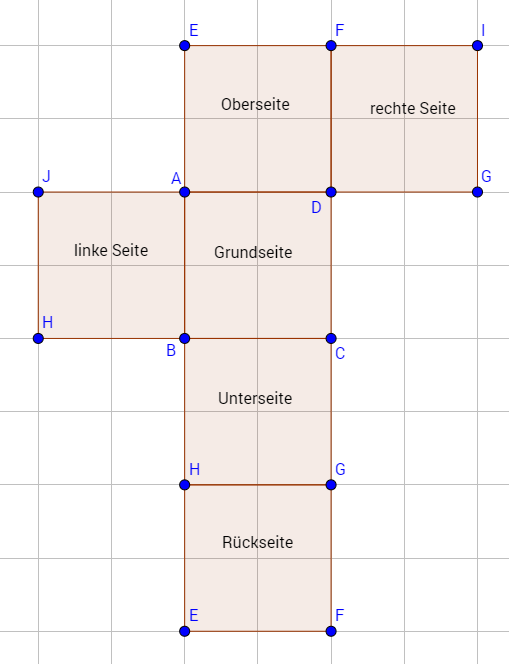
Wichtig ist nur, dass die Anzahl der Seiten sich nicht verändert und die Anzahl, die du am Anfang zusammengerechnet hast, immer mit der Lösung übereinstimmt.
Merke
Merke
Wir fassen zusammen:
Schrägbilder sind Abbildungen geometrischer Figuren.
Schrägbilder haben keine versteckten Ecken oder Kanten.
Um ein Schrägbild in ein Körpernetz zu verwandeln zählst du erst die Anzahl der Seiten und zerschneidest dann die Figur an einer Stelle. Danach legst du alles auf eine Ebene.
Es gibt mehr als eine Lösung für Körpernetze von Schrägbildern.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Teste dein Wissen!
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Mathematik? Dann vereinbare einen Termin bei einem Lehrer unserer Mathematik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Mathematik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Mathe-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema
Wir sind durchgehend für dich erreichbar
