Der Quader ist die erste dreidimensionale Figur, die man in der Schule kennenlernt. In diesem Lerntext werden wir die Figur auseinandernehmen, die Begrifflichkeiten klären und auch die ersten Formeln zur Berechnung einführen.
Was ist ein Quader?
Hier erhältst du einen schnellen Überblick über das Wichtigste zur dreidimensionalen Figur, dem Quader.
Methode
- Quader sind dir sicher schon im Alltag begegnet: Ein Würfel, ein Paket oder ein eingepacktes Geschenk sind Quader.
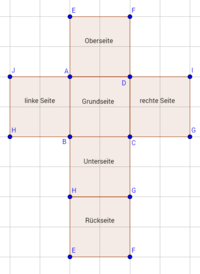
- Ein Quader hat 6 Flächen: die vordere Fläche, die hintere Fläche, die Deckfläche, die Grundfläche, die rechte und die linke Seitenfläche.
- Ein Quader kann breit und lang sein und die neue Dimension ist die Tiefe.
- Die Oberfläche berechnest du mit: $ Umfang\;=\;2 \cdot\; a*b\;+\;2\cdot\; a*c \;+\; 2 \cdot \;b*c$
- Das Volumen berechnest du mit: $Volumen \; = \; a \cdot b \cdot c$
Noch nicht alles klar? Du hast jetzt eine kleine Übersicht über den Quader erhalten. Wir möchten dir nun alles etwas detaillierter erklären damit du fit im Thema Quader wirst.
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
Quader - Die Flächen
Der Quader ist die erste Figur, die du in der Schulzeit kennen lernst, die nicht nur in zwei, sondern in drei Dimensionen dargestellt wird. Um einen Quader also zu zeichnen, benötigst du eine dritte Ebene, dein gewöhnliches Koordinatensystem reicht da nicht aus. Doch schauen wir uns erst einmal einen Quader an und bestimmen die Bezeichnungen, um es danach in einem Koordinatensystem einzeichnen zu können.
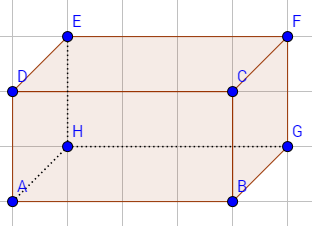
Jeder Quader besteht aus 8 Punkten, die verbunden werden. Der Quader hat verschiedene Seitenflächen, die auch verschiedene Namen bekommen. Die Seitenfläche zwischen den Punkten ABCD ist die Vorderseite. In der nächsten Abbildung sind alle wichtigen Begrifflichkeiten eingezeichnet:
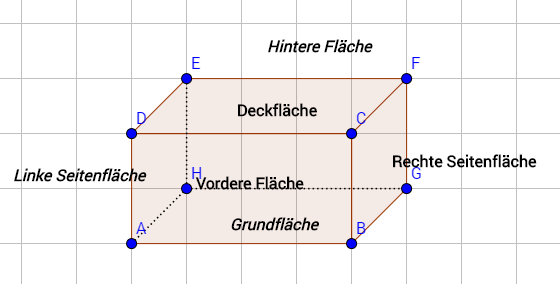
In der Abbildung sind die Begriffe für die sechs Seiten des Quaders eingezeichnet. Die Begriffe, die kursiv geschrieben sind, bezeichnen Seitenflächen, die sich im Hintergrund befinden. Klären wir einmal die Begrifflichkeiten:
Merke
Die Vorderseite, oder auch Vordere Fläche genannt, ist die Seite, auf die man direkt schaut. Sie wird in der Abbildung durch die Punkte ABCD verbunden.
Die Grundfläche ist die Fläche, auf der der Quader steht. Hier durch die Punkte ABGH verbunden.
Die Hintere Fläche liegt gegenüber der Vorderseite und wird in der Abbildung durch die Punkte EFGH verbunden.
Die Deckfläche, oder Deckelseite, ist die obere Seite im Quader. Sie liegt oben auf wie ein Deckel auf einem Topf. Sie wird hier durch die Punkte CDEF verbunden.
Die linke Seitenfläche ist die linke Seite an einem Quader. Sie wird hier durch die Punkte ADEH verbunden.
Die rechte Seitenfläche ist die rechte Seite an einem Quader. Sie wird in der Abbildung durch die Punkte BCFG verbunden.
Doch reichen die Bezeichnungen der Seitenflächen nicht aus, um mit Formeln rechnen zu können. Hierfür benötigen wir wichtige Seitenbezeichnungen, beispielsweise die Höhe. Diese Begrifflichkeiten sehen wir in der nächsten Abbildung:
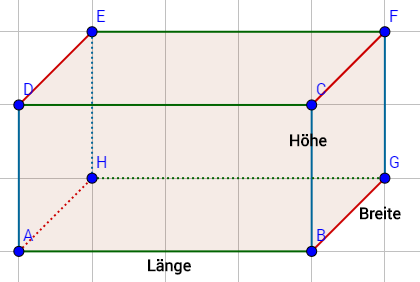
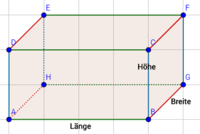
Jeder Quader besteht aus Seiten, die in drei verschiedene Richtungen zeigen, der Höhe, die senkrecht verläuft, wie die y-Achse in einem Koordinatensystem, die Länge, die der x-Achse in einem Koordinatensystem ähnelt und die dritte Seite, die Breite.
In der Abbildung haben wir jede Länge $\textcolor{green}{grün}$, jede Höhe $\textcolor{blue}{blau}$ und jede Breite $\textcolor{red}{rot}$ eingezeichnet.
Merke
Der Quader besteht aus drei verschiedenen Seiten.
Die Länge bezeichnet die waagerechten Seiten.
Die Höhe bezeichnet die senkrechten Seiten.
Die Breite bezeichnet alle Seiten, die nach "hinten" verlaufen.
Oberfläche und Volumen beim Quader berechnen
Jetzt haben wir alle wichtigen Seitenflächen und Seitenbezeichnungen kennen gelernt und können Formeln verwenden. Bekannt sollten dir von Rechtecken noch der Flächeninhalt und der Umfang sein. Diese Formeln können wir auch beim Quader gebrauchen, jedoch im dreidimensionalen Raum, somit mit anderen Bezeichnungen. Schauen wir uns nun an, wie wir die Oberfläche und das Volumen eines Quaders berechnen:
Um also die Oberfläche eines Quaders auszurechnen, benötigen wir folgende Formel:
$Oberfläche\;=\; Fläche1\;+ \;Fläche2\; +\; Fläche3\; +\; Fläche4\; +\; Fläche5 \;+\; Fläche6$
Vereinfacht ergibt sich: $Oberfläche\;=\;2 \cdot \;Fläche1+ \;2 \cdot \;Fläche2 \;+\;2 \cdot \;Fläche3$
Die Seitenflächen gruppieren sich hierbei in gegenüberliegende Seitenflächen, also gehören die vordere Seite und die hintere Seite zusammen. Genauso gruppieren sich linke und rechte Seitenfläche, als auch Deckfläche und Grundfläche.
Merke
Oberfläche eines Quaders:
$ Umfang\;=\;2 \cdot\; a*b\;+\;2\cdot\; a*c \;+\; 2 \cdot \;b*c$
Wobei a die Länge, b die Höhe und c die Breite ist.
Das Volumen entspricht dem Flächeninhalt bei zweidimensionalen Figuren und wird auch genauso gebildet. Möchtest du nun das Volumen eines Quaders berechnen, multiplizierst du die drei Seiten miteinander:
Merke
Das Volumen eines Quaders ist:
$Volumen \; = \; a \cdot b \cdot c$
Wobei a die Länge, b die Höhe und c die Breite ist.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wird dir viel Spaß und Erfolg!
Teste dein Wissen! Übungsaufgaben
Du brauchst mehr Hilfe? Wir unterstützen Dich!
Bewertung bundesweit
Unsere Kunden über den Studienkreis Feedback von Eltern & Schüler:innen
Studienkreis Nachhilfe Deutschland:
4.60 / 5.00 Sterne bei 3700 Bewertungen
Weitere Erklärungen & Übungen zum Thema Mathematik > Geometrie
Klassenstufen in Mathematik
Weitere Fächer Lernen und Üben
Noch Fragen? Wir sind durchgehend für dich erreichbar
