Bewegungsenergie berechnen - Definition, Formel und Beispiele
In diesem Text erklären wir dir, was man unter der Bewegungs- bzw. kinetischen Energie versteht und wie du diese berechnen kannst. Dafür werden wir einige Begriffe anführen und erklären, die du für die Berechnung benötigst. Unseren Text über die Lageenergie solltest du im Vorfeld gelesen haben.
Was ist Bewegungsenergie?
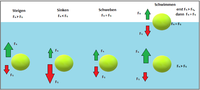
Die Bewegungsenergie wird oftmals auch kinetische Energie genannt. Das liegt unter anderem daran, dass diese Energieform bei sich bewegenden Körpern zu finden ist. Das Bewegungsenergiepotenzial, das ein Körper hat, wird durch die Höhe bestimmt, in der sich dieser befindet, freigesetzt wird es, wenn diese Höhe reduziert wird.
Gut zu wissen
Der Begriff Kinetik leitet sich von dem griechischen Wort kinesis ab, das so viel wie Bewegung bedeutet.
Die kinetischen Energie eines sich bewegenden Körpers kann durch die folgende Formel berechnet werden:
Merke
$E_{kin}=\frac{1}{2}\cdot{m}\cdot{v^2}$
In dieser Formel wird die halbe Masse des sich bewegenden Objekts $(\frac{1}{2}\cdot{m})$ mit der Geschwindigkeit zum Quadrat $(v^2)$ multipliziert. Die Einheit der Bewegungsenergie ist Joule ($J$).
- Über 700 Lerntexte & Videos
- Über 250.000 Übungen & Lösungen
- Gratis Nachhilfe-Probestunde
Beispiele zur Berechnung von Bewegungsenergie
Beispiel
Schauen wir uns das an einem Beispiel an:
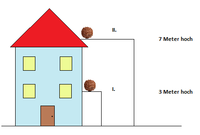
Eine Physikklasse eines Gymnasiums möchte berechnen, wie sich der Fall einer Kokosnuss aus unterschiedlichen Höhen auf diese auswirkt. Dazu soll eine der Nüsse aus dem ersten Stock ihres Schulgebäudes geworfen werden und eine weitere dann vom Dach aus. Die Klasse soll zuerst berechnen, welche verschiedenen Energieniveaus die Kokosnüsse bei ihrem Fall haben.
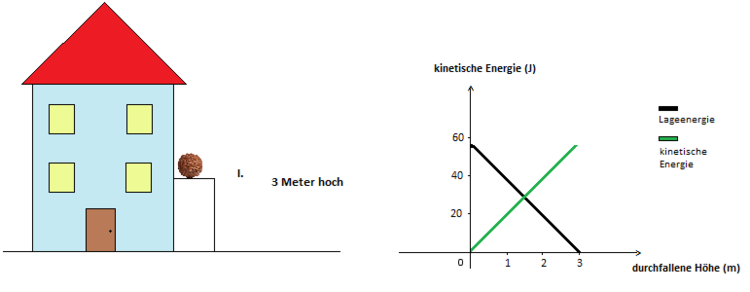
Wie du in der Grafik sehen kannst, wird die erste Kokosnuss aus einer Höhe von drei Metern fallen gelassen. Das Bewegungsenergieniveau der Nuss während des Falls kannst du direkt daneben sehen. Wie du feststellen kannst, nimmt die Bewegungsenergie (kinetische Energie) mit zunehmender durchfallener Höhe zu, während die Lageenergie (potenzielle Energie) mit zunehmender durchfallener Höhe abnimmt. Nun wollen wir uns ansehen, wie du das Niveau der Energie berechnen kannst.
Merke
Die Formel für die Errechnung des Niveaus der potenziellen Energie ergibt sich aus den Faktoren der Höhe ($h$), die in Metern ($m$) angegeben wird, der Masse ($m$) des Objekts, die in Kilogramm ($kg$) angegeben wird und der Konstante der Erdbeschleunigung ($g$) mit der Einheit $\frac{m}{s^2}$. Diese drei Faktoren werden multipliziert, um die potzenzielle Energie ($E_{pot}$) welche bei ruhenden Körpern der kinetischen Energie ($E_{kin}$) entspricht, zu ermitteln.
$E_{pot} = {m}\cdot{g}\cdot{h}$ (nur für ruhende Körper)
Wird die Kokusnuss nun fallen gelassen, sinkt die potenzielle Energie und die kinetische Energie steigt, bis sie ihr Maximum erreicht hat und somit die potenzielle Energie in kinetische Energie umgewandelt wurde. Die Formel für die Errechnung des Niveaus der kinetischen Energie ergibt sich aus den Faktor ($\frac{1}{2}$) welcher mit der Masse ($m$) des Objekts, die in Kilogramm ($kg$) angegeben wird und der Geschwindigkeit zum Quadrat ($v^2$), die in ($\frac{m^2}{s^2}$) angegeben wird, multipliziert.
$E_{kin}=\frac{1}{2}\cdot{m}\cdot{v^2}$ (in Bewegung befindlicher Körper)
Wenn wir diese Formeln nun auf unser Beispiel anwenden und davon ausgehen, dass die Kokosnuss eine Masse von 2 kg hat, erhältst du folgende Rechnung:
$E_{pot}= {2kg}\cdot{9,81}\frac{m}{s^2}\cdot{3m}$ = $58,86 J$
Wenn du diese Formel ausrechnest, bekommst du das potenzielle Energieniveau der Kokosnuss zu Beginn. Dieses ist natürlich nur theoretisch, solange sich die Nuss in unserem Beispiel nicht bewegt. Die beim Fall freigesetzte Energie wird dann in der Geschwindigkeit sichtbar, die während des Fluges entsteht. Schauen wir uns nun einmal an, wie du diese Geschwindigkeit berechnen kannst.
Wir betrachten unsere, am Anfang genannte, Formel für die kinetische Energie: $E_{kin}=\frac{1}{2}\cdot{m}\cdot{v^2}$ Stellen wir diese nun einmal so um, dass wir direkt die Geschwindigkeit berechnen können. Du erhältst dann folgende Formel:
$v=\sqrt[]{\frac{2\cdot{E_{kin}}}{m}}$
Setzen wir als nächstes die uns bereits bekannten Werte aus der Berechnung oben ein, um zu erfahren, mit welcher Geschwindigkeit die Kokosnuss fällt.
$v=\sqrt[]{\frac{2\cdot{58,86J}}{2kg}}$
Die Geschwindigkeit die du bei dieser Rechnung erhältst, wird in Meter pro Sekunde $(\frac{m}{s})$ angegeben. In unserem Beispiel ergibt sich für die fallende Kokosnuss eine Geschwindigkeit von $7,672 \frac{m}{s}$.
Die Höhe des kinetischen Energieniveaus und die Fallgeschwindigkeit eines Objekts, hängen von der Höhe des Startpunktes ab.
Man kann also festhalten, dass, je höher ein Objekt gelagert ist, desto höher ist die im Flug freigesetzte kinetische Energie und die Geschwindigkeit.
Wird diese anschließend aus einer Höhe von drei Metern mit einer Geschwindigkeit von $7,672 \frac{m}{s}$ zu Boden fallen gelassen erhälst du folgende Rechnung:
$E_{kin}=\frac{1}{2}\cdot 2kg \cdot (7,672\frac{m}{s})^2$ = $58,86 J$
Ein Vergleich mit der potenziellen Energie zeigt, dass diese vollständig in kinetische Energie umgewandelt wurde.
Gut zu wissen
Bitte beachte, neben unserem Beispiel der fallenden Kokusnuss gibt es auch noch andere Ursachen für die Bewegung eines Körpers wie z.B Federkräfte, Treibladungen, Motorkraft, Rückstoßkraft und viele mehr.
Nun weißt du, was unter dem Begriff der Bewegungsenergie bzw. kinetischen Energie zu verstehen ist und wie man das Niveau dieser Energieform und die Geschwindigkeit eines sich bewegenden Objekts berechnen kann. Dein neu erlerntes Wissen kannst du nun an unseren Übungsaufgaben austesten. Dabei wünschen wir dir viel Spaß und Erfolg!
Teste dein Wissen!
Ein Katzenbesitzer hat eine teure Vase auf einem Schrank (1,2 Meter hoch) stehen. Die Vase wiegt $6 kg$. In seiner Abwesenheit springt seine Katze auf den Schrank und schubst die Vase dabei hinunter. Sie fällt mit einer Geschwindigkeit von $4,85 \frac{m}{s}$ auf den Boden. Wie hoch ist das kinetische Energieniveau dieser Vase?
Welche der folgenden Maßeinheiten werden für die kinetische Energie verwendet?
Mit wenigen Klicks die passenden Aufgaben und Lösungen zum Üben und Selbst-Lernen finden.
Hol dir Hilfe beim Studienkreis!
Selbst-Lernportal Online
Zugriff auf alle Aufgaben erhältst du in unserem Selbst-Lernportal. Bei Fragen helfen dir unsere Lehrer der online Hausaufgabenhilfe - sofort ohne Termin!
- Online-Chat 14-20 Uhr
- 700 Lerntexte & Videos
- Über 250.000 Übungsaufgaben
Einzelnachhilfe Online
Du benötigst Hilfe in Physik? Dann vereinbare einen Termin bei einem Lehrer unserer Physik-Nachhilfe Online. Lehrer zum Wunschtermin online fragen!
- Online-Nachhilfe
- Zum Wunschtermin
- Geprüfte Physik-Nachhilfelehrer
Nachhilfe in deiner Nähe
Du möchtest Hilfe von einem Lehrer der Physik-Nachhilfe aus deiner Stadt erhalten? Dann vereinbare einen Termin in einer Nachhilfeschule in deiner Nähe.
- Nachhilfe in deiner Nähe
- Zum Wunschtermin
- Geprüfte Physik-Nachhilfelehrer
Unsere Kunden über den Studienkreis
Weitere Erklärungen & Übungen zum Thema